Tests on the Value at Risk

Author

Affiliation

Beniamino Sartini

University of Bologna

library(dplyr)
library(latex2exp)
library(backports)
library(ggplot2)
library(knitr)

Let’s consider a Gaussian AR(2)-GARCH(1,2) model defined as: $$\begin{array}{rl}& x_t=\mu +{\varphi }_1{x}_{t-1}+{\varphi }_2{x}_{t-2}+e_t\text{,}\\ & e_t={\sigma }_t{u}_t\text{,}\\ & {\sigma }_t^2=\omega +{\alpha }_1{e}_{t-1}^2+{\beta }_1{\sigma }_{t-1}^2+{\beta }_2{\sigma }_{t-2}^2\text{.}\end{array}$$ The Value at Risk (VaR) at a confidence level $\alpha$ is time dependent and implicitly defined as: $$\mathbb{P}\{X_t\le {\text{VaR}}_{t|t-1}^{\alpha }|I_{t-1})=\alpha \text{.}$$ The distribution of $x_t$ is normal with conditional moments given by: $$\{\begin{array}{l}\mathbb{E}\{X_t|I_{t-1}\}=\mu +{\varphi }_1{x}_{t-1}+{\varphi }_2{x}_{t-1}\\ \mathbb{V}\{X_t|I_{t-1}\}=\omega +{\alpha }_1{e}_{t-1}^2+{\beta }_1{\sigma }_{t-1}^2+{\beta }_2{\sigma }_{t-2}^2\end{array}$$ Hence, given the quantile of a standard normal, namely $q^{\alpha }$ the Value at Risk can be simply computed as: $${\text{VaR}}_{t|t-1}^{\alpha }=\mathbb{E}\{X_t|I_{t-1}\}+q^{\alpha }\sqrt{\mathbb{V}\{X_t|I_{t-1}\}}\text{.}$$

1 Test on the number of violations

Let’s define a violation of the ${\text{VaR}}_{t|t-1}^{\alpha }$ as $$v_t={\mathbb{1}}_{[x_t\le {\text{VaR}}_{t|t-1}^{\alpha }]}\sim \text{Bernoulli}(\alpha )\text{,}$$

and let’s define the number of violations of the conditional VaR as follows, i.e. $$N_t=\sum _{i=1}^t{v}_i\text{.}$$

1.1 Asymptotic variance

Applying the central limit theorem (CLT) it is possible to prove that the statistic test converges in distribution to a standard normal, i.e. $$N{V}_1=\frac{1}{\sqrt{t}}\sum _{i=1}^t\left(\frac{v_i-\alpha }{\sqrt{\alpha (1-\alpha )}}\right)\underset{n\to \mathrm{\infty }}{\stackrel{d}{⟶}}\mathcal{N}(0,1)\text{.}$$ Hence, given the null hypothesis $H_0:\mathbb{P}\{X_t\le {\text{VaR}}_{t|t-1}^{\alpha }|I_{t-1})=\alpha$, that is equivalent to $\mathbb{E}\{e_t\}=\alpha$ we define the critical values at a confidence level ${\alpha }^{\ast }$ as $$\begin{array}{rl}\alpha & =\mathbb{P}\{|N{V}_1|>t_{{\alpha }^{\ast }/2}\}\\ \Updownarrow & \\ t_{{\alpha }^{\ast }/2}& ={\mathbb{P}}^{-1}\{\mathbb{P}\{|N{V}_1|>t_{{\alpha }^{\ast }/2}\}\}\end{array}$$

where $\mathbb{P}$ and ${\mathbb{P}}^{-1}$ are respectively the distribution and the quantile of a standard normal. Therefore, the null hypothesis is rejected at a confidence level ${\alpha }^{\ast }$ if: $$\{\begin{array}{l}[N{V}_1<-t_{{\alpha }^{\ast }/2}]\cup [N{V}_1>t_{{\alpha }^{\ast }/2}]H_0\text{ rejected}\\ [-t_{{\alpha }^{\ast }/2}<N{V}_1<t_{{\alpha }^{\ast }/2}]H_0\text{ non rejected}\end{array}$$

1.2 Empirical variance

Instead of using the theoretical variance of $e_t$, namely $\alpha (1-\alpha )$, let’s substitute it with the empirical one, i.e. $$\alpha (1-\alpha )⟶\frac{N_t}{t}(1-\frac{N_t}{t})\text{.}$$ Hence, the new statistic test $N{V}_2$ converges to $N{V}_1$ in probability, therefore also in distribution, i.e.  $$N{V}_2=\frac{1}{\sqrt{t}}\sum _{i=1}^t\left(\frac{v_i-\alpha }{\sqrt{\frac{N_t}{t}(1-\frac{N_t}{t})}}\right)\underset{n\to \mathrm{\infty }}{\stackrel{p}{⟶}}N{V}_1\underset{n\to \mathrm{\infty }}{\stackrel{d}{⟶}}\mathcal{N}(0,1)\text{.}$$

For small samples, the following relation between the two statistics should be used: $$N{V}_2=\frac{\sqrt{\alpha (1-\alpha )}}{\sqrt{\frac{N_t}{t}(1-\frac{N_t}{t})}}N{V}_1\text{.}$$

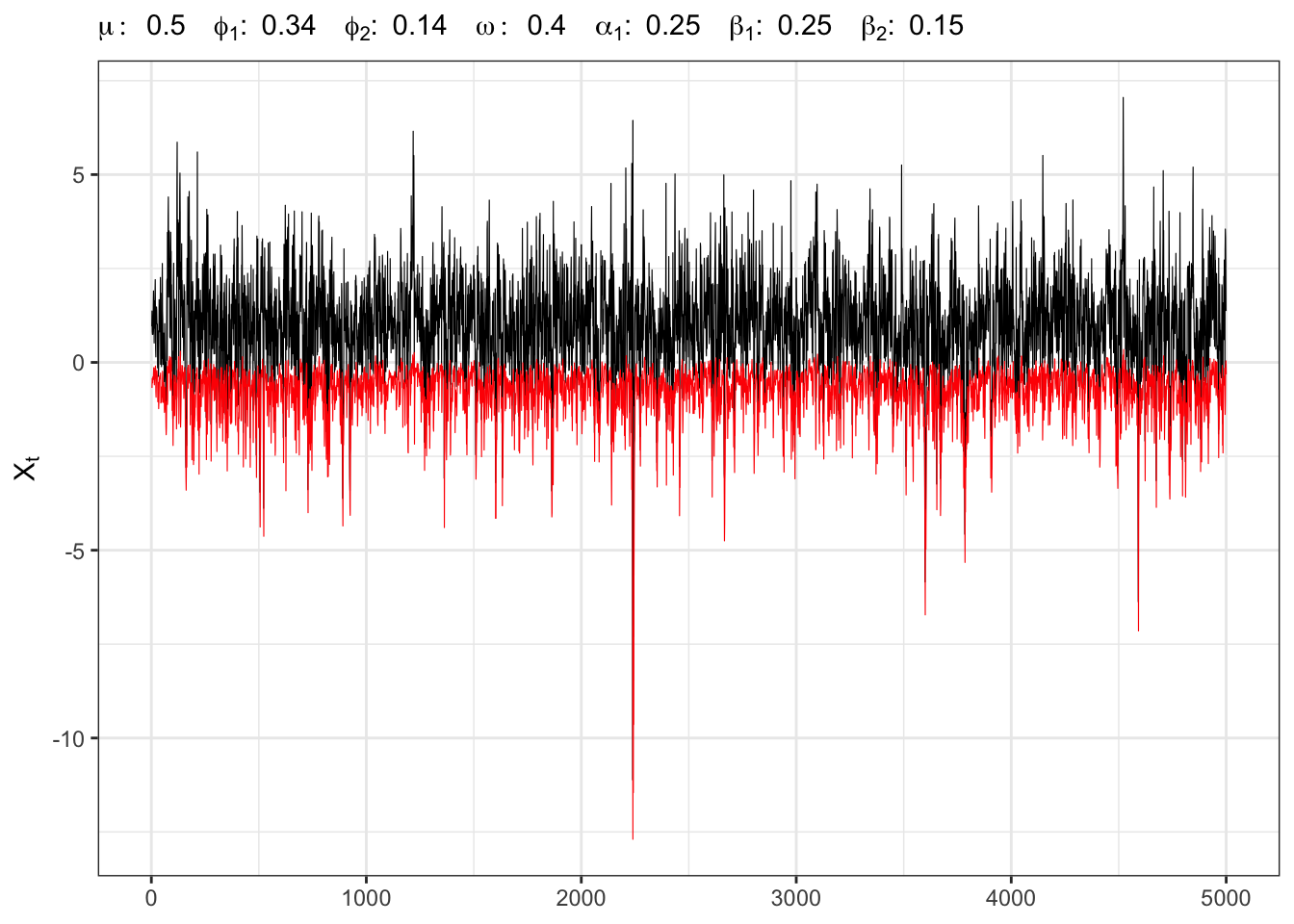
2 Example: $H_0$ is not rejected

Instead of simulating exactly $u_t\sim \mathcal{N}(0,1)$, let’s simulate residuals that are close to the normal distribution, i.e. $u_t\sim \mathcal{t}(25)$.

# ===================== Setups ======================
set.seed(1)   # random seed 
ci <- 0.05    # confidence level 
t_bar <- 5000 # number of simulations 
# parameters
parAR <- c(mu=0.5, phi1 = 0.34, phi1 = 0.14)
parGARCH <- c(omega=0.4, alpha1=0.25, 
              beta1=0.25, beta2=0.15) 
# long-term std deviation of residuals 
sigma_eps <- sqrt(parGARCH[1]/(1-sum(parGARCH[-1])))
# ================== Simulation =====================
# Initial points
Xt <- rep(parAR[1]/(1-sum(parAR[-1])), 3)
sigma <- rep(sigma_eps, 3)
# Simulated residuals 
eps <- rt(t_bar, 25)
eps[1:3] = eps[1:3]*sigma_eps
# Value at Risk
q_alpha = qnorm(ci)
VaR = c(0)
for(t in 3:t_bar){
  # AR component 
  Xt[t] <- parAR[1] + parAR[2]*Xt[t-1] + parAR[3]*Xt[t-2]
  # ARCH component 
  sigma[t] <- parGARCH[1] + parGARCH[2]*eps[t-1]^2 
  # GARCH component 
  sigma[t] <- sigma[t] + parGARCH[3]*sigma[t-1]^2 + parGARCH[4]*sigma[t-2]^2
  sigma[t] <- sqrt(sigma[t])
  # Simulated residuals 
  eps[t] <- sigma[t]*eps[t]
  # Simulated value at risk
  VaR[t] <- Xt[t] + sigma[t]*q_alpha
  # Simulated time series 
  Xt[t] <- Xt[t] + eps[t]
}
# ===================== Plot ======================
# GARCH(1,1) simulation
ggplot()+
  geom_line(aes(1:t_bar, Xt), size = 0.2)+
  geom_line(aes(1:t_bar, VaR), size = 0.2, color = "red")+
  theme_bw()+
  labs(x = NULL, y = TeX("$X_t$"),
       subtitle = TeX(paste0("$\\mu:\\;", parAR[1], 
                             "\\;\\; \\phi_{1}:\\;", parAR[2],
                             "\\;\\; \\phi_{2}:\\;", parAR[3],
                             "\\;\\; \\omega:\\;", parGARCH[1], 
                             "\\;\\; \\alpha_{1}:\\;", parGARCH[2],
                             "\\;\\; \\beta_{1}:\\;", parGARCH[3],
                             "\\;\\; \\beta_{2}:\\;", parGARCH[4],
                             "$")))

Figure 1: AR(2)-GARCH(1,2) simulation with theoric (red) VaR at $\alpha =0.05$.

# ======================================
# Violation of the VaR
vt <- ifelse(Xt < VaR, 1, 0)
vt[1:3] <- 0
# Theoric variance
v_theoric <- ci*(1-ci)
# Empiric variance
v_empiric <- (sum(vt)/t_bar)*(1 - sum(vt)/t_bar)
# Standardized number of violations
Nt <- sum((vt - ci)/sqrt(v_theoric))
# Statistic test (NV_1)
NV1 <- (1/sqrt(t_bar))*Nt
# Statistic test (NV_2)
NV2 <- (sqrt(v_theoric)/sqrt(v_empiric))*NV1
# Rejection level 
t_alpha <- qnorm(ci/2)
# =============== Kable =============== 
kab <- dplyr::tibble(
  n = t_bar,
  alpha = paste0(format(ci*100, digits = 3), "%"),
  alpha_hat = paste0(format(sum(vt)/t_bar*100, digits = 3), "%"),
  t_alpha_dw = t_alpha,
  NV1 = NV1,
  NV2 = NV2,
  t_alpha_up = -t_alpha,
  H01 = ifelse(NV1 > t_alpha_up | NV1 < t_alpha_dw, "Rejected", "Non-Rejected"),
  H02 = ifelse(NV2 > t_alpha_up | NV2 < t_alpha_dw, "Rejected", "Non-Rejected")
)  %>%
  dplyr::mutate_if(is.numeric, format, digits = 4, scientific = FALSE)
colnames(kab) <- c("$$n$$", "$$\\alpha$$", "$$\\frac{N_n}{n}$$", "$$-t_{\\alpha/2}$$", 
                   "$$NV_1$$", "$$NV_2$$", "$$t_{\\alpha/2}$$", "$$H_0(NV_1)$$", "$$H_0(NV_2)$$")
knitr::kable(kab, booktabs = TRUE ,escape = FALSE, align = 'c')%>%
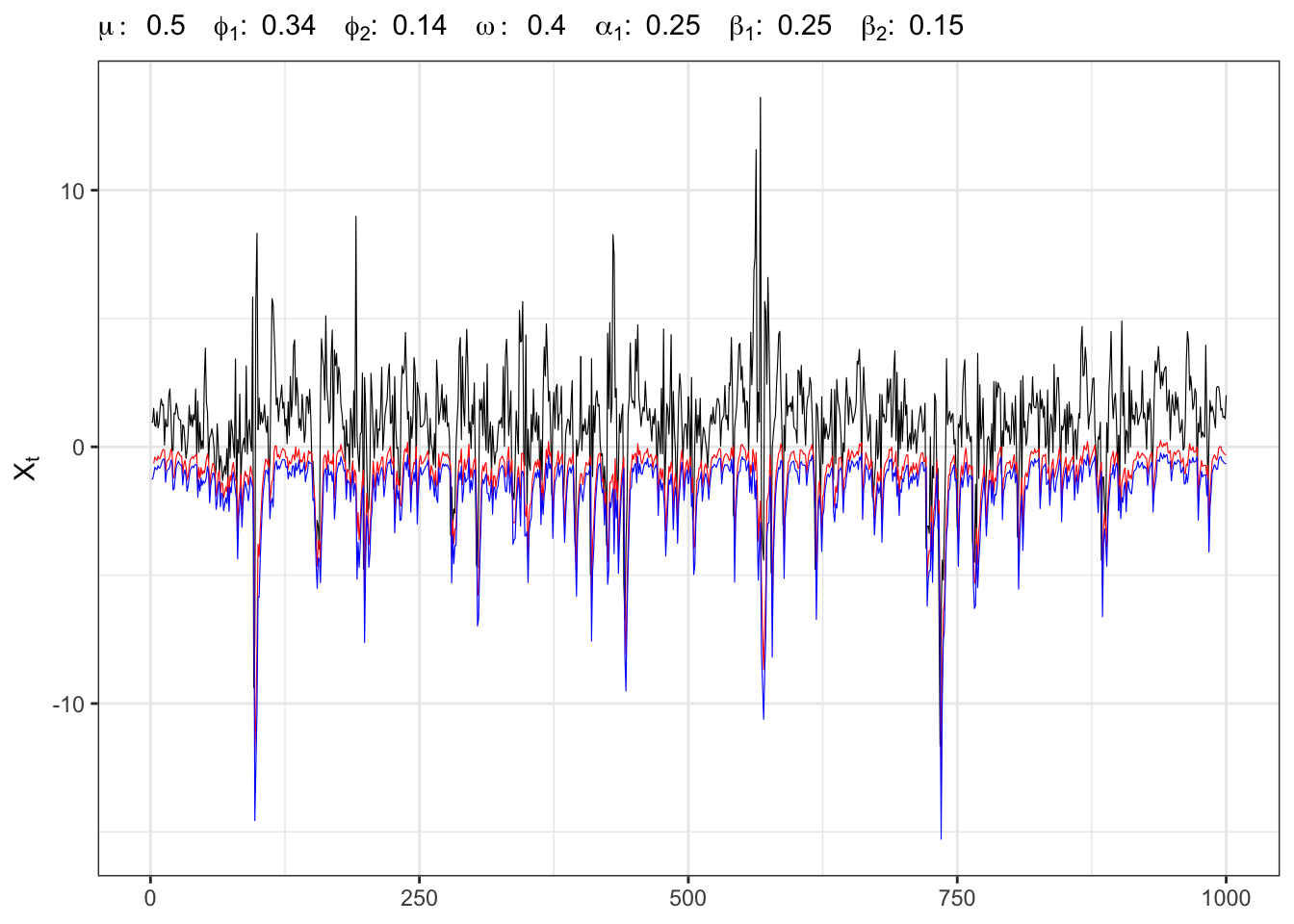
  kableExtra::row_spec(0, color = "white", background = "green") 

Table 1: Test for a Student-$t$ with 25 degrees of freedom at ${\alpha }^{\ast }=0.05$ on the number of violations of the theoric VaR at $\alpha =0.05$.

$$n$$	$$\alpha$$	$$\frac{N_n}{n}$$	$$-t_{\alpha /2}$$	$$N{V}_1$$	$$N{V}_2$$	$$t_{\alpha /2}$$	$$H_0(N{V}_1)$$	$$H_0(N{V}_2)$$
5000	5%	5.6%	-1.96	1.947	1.845	1.96	Non-Rejected	Non-Rejected

3 Example: $H_0$ is rejected

Instead of simulating exactly $u_t\sim \mathcal{N}(0,1)$, let’s simulate residuals that are not close to the normal distribution, i.e. $u_t\sim \mathcal{t}(5)$.

# ==================== Setups =====================
set.seed(1)   # random seed 
ci <- 0.05    # confidence level 
t_bar <- 1000 # number of simulations 
# parameters
parAR <- c(mu=0.5, phi1 = 0.34, phi1 = 0.14)
parGARCH <- c(omega=0.4, alpha1=0.25,
              beta1=0.25, beta2=0.15) 
# quasi long-term std deviation of residuals 
sigma_eps <- sqrt(parGARCH[1]/(1-sum(parGARCH[-1])))
# ================== Simulation ===================
set.seed(1)
# Initial points
Xt <- rep(parAR[1]/(1-sum(parAR[-1])), 3)
mu <- rep(parAR[1]/(1-sum(parAR[-1])), 3)
sigma <- rep(sigma_eps, 3)
# Simulated residuals 
eps <- rt(t_bar, 5) 
eps[1:3] <- eps[1:3]*sigma_eps
# Value at Risk
q_alpha = qnorm(ci)
VaR = c(0)
for(t in 3:t_bar){
  # AR component 
  mu[t] <- parAR[1] + parAR[2]*Xt[t-1] + parAR[3]*Xt[t-2]
  # ARCH component 
  sigma[t] <- parGARCH[1] + parGARCH[2]*eps[t-1]^2 
  # GARCH component 
  sigma[t] <- sigma[t] + parGARCH[3]*sigma[t-1]^2 + parGARCH[4]*sigma[t-2]^2
  sigma[t] <- sqrt(sigma[t])
  # Simulated residuals 
  eps[t] <- sigma[t]*eps[t]
  # Simulated value at risk
  VaR[t] <- mu[t] + sigma[t]*q_alpha
  # Simulated time series 
  Xt[t] <- mu[t] + eps[t]
}
# Empirical quantile 
q_alpha_emp <- quantile(eps/sigma, probs = ci)
VaR_emp <- mu + sigma*q_alpha_emp

# ===================== Plot ======================
# GARCH(1,1) simulation
ggplot()+
  geom_line(aes(1:t_bar, Xt), size = 0.2)+
  geom_line(aes(1:t_bar, VaR), size = 0.2, color = "red")+
  geom_line(aes(1:t_bar, VaR_emp), size = 0.2, color = "blue")+
  theme_bw()+
  labs(x = NULL, y = TeX("$X_t$"),
       subtitle = TeX(paste0("$\\mu:\\;", parAR[1], 
                             "\\;\\; \\phi_{1}:\\;", parAR[2],
                             "\\;\\; \\phi_{2}:\\;", parAR[3],
                             "\\;\\; \\omega:\\;", parGARCH[1], 
                             "\\;\\; \\alpha_{1}:\\;", parGARCH[2],
                             "\\;\\; \\beta_{1}:\\;", parGARCH[3],
                             "\\;\\; \\beta_{2}:\\;", parGARCH[4],
                             "$")))

Figure 2: AR(2)-GARCH(1,2) simulation with theoric (red) and empirical (blue) VaR at $\alpha =0.05$.

Computing the test on the normal quantile gives a rejection of the null hypothesis $H_0$, i.e. the deviation from the VaR is not stochastic and it is not an adequate measure of risk.

# ======================================
# Violation of the VaR
vt <- ifelse(Xt < VaR, 1, 0)
vt[1:3] <- 0
# Theoric variance
v_theoric <- ci*(1-ci)
# Empiric variance
v_empiric <- (sum(vt)/t_bar)*(1 - sum(vt)/t_bar)
# Standardized number of violations
Nt <- sum((vt - ci)/sqrt(v_theoric))
# Statistic test (NV_1)
NV1 <- (1/sqrt(t_bar))*Nt
# Statistic test (NV_2)
NV2 <- (sqrt(v_theoric)/sqrt(v_empiric))*NV1
# Rejection level 
t_alpha <- qnorm(ci/2)
# =============== Kable =============== 
kab <- dplyr::tibble(
  n = t_bar,
  alpha = paste0(format(ci*100, digits = 3), "%"),
  alpha_hat = paste0(format(sum(vt)/t_bar*100, digits = 3), "%"),
  t_alpha_dw = t_alpha,
  NV1 = NV1,
  NV2 = NV2,
  t_alpha_up = -t_alpha,
  H01 = ifelse(NV1 > t_alpha_up | NV1 < t_alpha_dw, "Rejected", "Non-Rejected"),
  H02 = ifelse(NV2 > t_alpha_up | NV2 < t_alpha_dw, "Rejected", "Non-Rejected")
)  %>%
  dplyr::mutate_if(is.numeric, format, digits = 4, scientific = FALSE)
colnames(kab) <- c("$$n$$", "$$\\alpha$$", "$$\\frac{N_n}{n}$$", "$$-t_{\\alpha/2}$$", 
                   "$$NV_1$$", "$$NV_2$$", "$$t_{\\alpha/2}$$", "$$H_0(NV_1)$$", "$$H_0(NV_2)$$")
knitr::kable(kab, booktabs = TRUE ,escape = FALSE, align = 'c')%>%
  kableExtra::row_spec(0, color = "white", background = "green") 

Table 2: Test for a Student-$t$ with 5 degrees of freedom at ${\alpha }^{\ast }=0.05$ on the number of violations of the theoric VaR at $\alpha =0.05$.

$$n$$	$$\alpha$$	$$\frac{N_n}{n}$$	$$-t_{\alpha /2}$$	$$N{V}_1$$	$$N{V}_2$$	$$t_{\alpha /2}$$	$$H_0(N{V}_1)$$	$$H_0(N{V}_2)$$
1000	5%	8.5%	-1.96	5.078	3.969	1.96	Rejected	Rejected

Setting $\alpha =0.05$ we obtain an empiric ${\hat{q}}_{\alpha }$ equal to -2.07 different from the theoric one of -1.6449.

4 VaR for $\text{BTC}$

From the series of close prices $P_t$, let’s compute the log-returns as: $$R_t=\log \left(\frac{P_t}{P_{t-1}}\right)=\log (P_t)-\log (P_{t-1})$$ Then, we fit a GARCH(2,3) on the log-returns, i.e. $$\begin{array}{rl}& x_t=\mu +e_t\\ & e_t={\sigma }_t{u}_t\\ & {\sigma }_t^2=\omega +\sum _{i=1}^2{\alpha }_i{e}_{t-i}^2+\sum _{j=1}^3{\beta }_j{\sigma }_{t-j}^2\end{array}$$ under the assumption of $u_t\sim \mathcal{N}(0,1)$.

library(rugarch)
ci <- 0.05    # confidence level 
# library(binancer) download prices 
load("../../../databases/data/temporary/crypto_prices.RData")
#btcusdt <- binancer::binance_klines("BTCUSDT", api = "spot", interval = "1d", 
#                                    from = "2018-01-01", to = Sys.Date()) 
# log close prices
btcusdt$log_Pt <- log(btcusdt$close)
# log returns 
btcusdt$Rt <- c(0, diff(btcusdt$log_Pt))
# In sample estimate 
data <- dplyr::filter(btcusdt, date <= as.POSIXct("2024-01-01"))
# Test 
data_test <- dplyr::filter(btcusdt, date >= as.POSIXct("2023-12-01"))

# GARCH Model
# Variance specification
GARCH_spec <- rugarch::ugarchspec(
    variance.model = list(model = "sGARCH", garchOrder = c(2,3), external.regressors = NULL),
    mean.model = list(armaOrder = c(0,0), include.mean = FALSE), distribution.model = "norm")
# Fitted model
GARCH_model <- rugarch::ugarchfit(data = data$Rt, spec = GARCH_spec, out.sample = 0)
# Fitted variance
data$sigma2 <- GARCH_model@fit$var
# Fitted standard deviation
data$sigma <- sqrt(data$sigma2)
# Standardized residuals
data$ut <- data$Rt/data$sigma

kab <- as_tibble(t(as_tibble(GARCH_model@fit$coef)))%>%
  dplyr::mutate_if(is.numeric, format, digits = 4, scientific = FALSE)
colnames(kab) <- c("$$\\omega$$", "$$\\alpha_1$$", "$$\\alpha_2$$", 
                   "$$\\beta_1$$", "$$\\beta_2$$", "$$\\beta_3$$")
knitr::kable(kab, booktabs = TRUE ,escape = FALSE, align = 'c')%>%
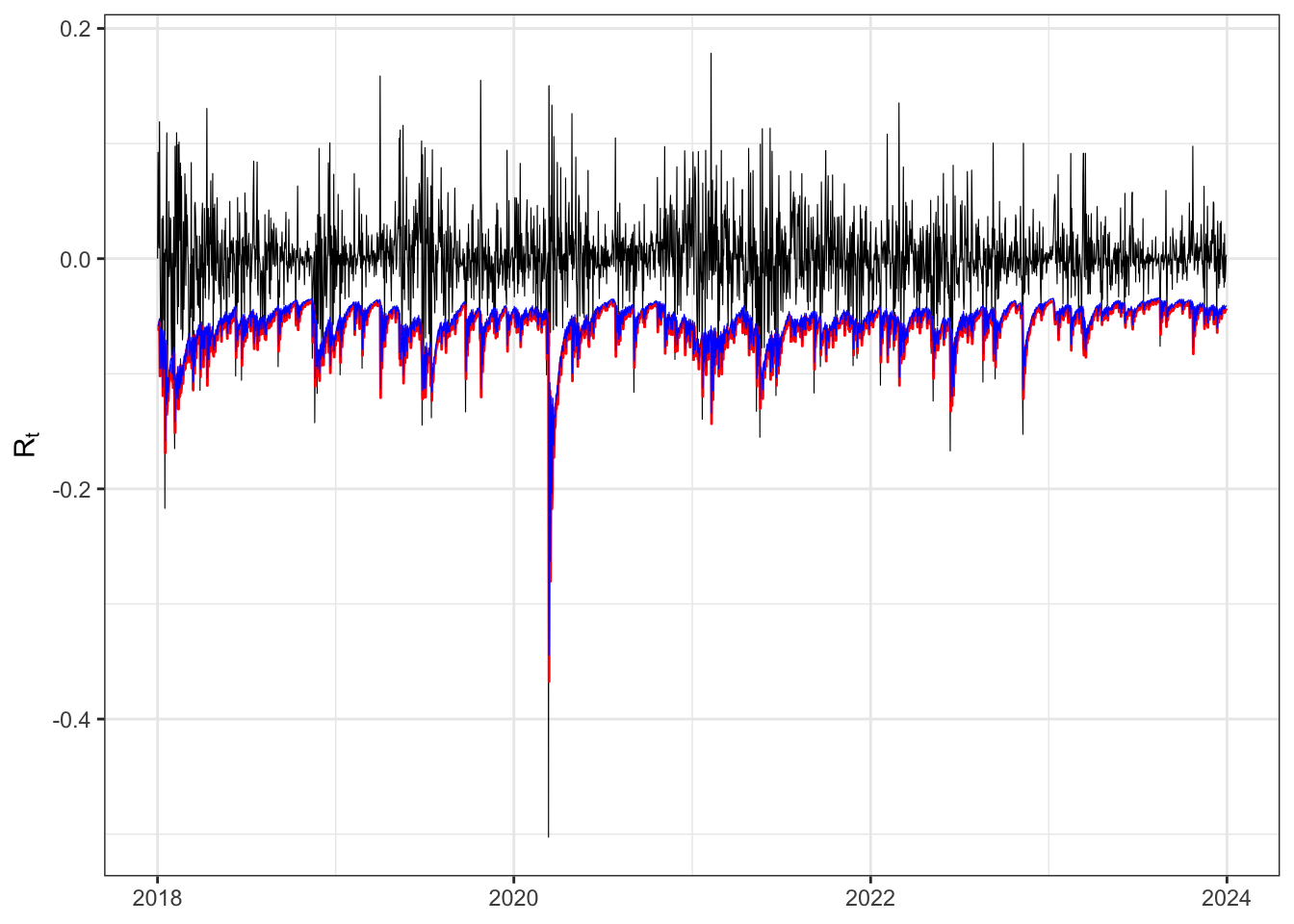
  kableExtra::row_spec(0, color = "white", background = "green") 

Table 3: Estimated GARCH(2,3) parameters on $\text{BTC}$ log-returns.

$$\omega$$	$${\alpha }_1$$	$${\alpha }_2$$	$${\beta }_1$$	$${\beta }_2$$	$${\beta }_3$$
0.0001155	0.1929	0.00000009728	0.1843	0.00000004144	0.5573

ggplot(data)+
  geom_line(aes(date, sigma))+
  theme_bw()

Figure 3: GARCH(2,3) std. deviation of $\text{BTC}$ log-returns.

VaR <- qnorm(0.05)*data$sigma
VaR_emp <- quantile(data$ut, probs = 0.05)*data$sigma
ggplot(data)+
  geom_line(aes(date, Rt), size = 0.2)+
  geom_line(aes(date, VaR), color = "red")+
  geom_line(aes(date, VaR_emp), color = "blue", size = 0.2)+
  theme_bw()+
  labs(x = NULL, y = TeX("$R_t$"))

Figure 4: Empirical VaR (red) and theoric VaR (blue) at ${\alpha }^{\ast }=0.05$ for $\text{BTC}$ log-returns.

# ======================================
Xt <- data$Rt
t_bar <- nrow(data)
# Violation of the VaR
vt <- ifelse(Xt < VaR, 1, 0)
vt[1:3] <- 0
# Theoric variance
v_theoric <- ci*(1-ci)
# Empiric variance
v_empiric <- (sum(vt)/t_bar)*(1 - sum(vt)/t_bar)
# Standardized number of violations
Nt <- sum((vt - ci)/sqrt(v_theoric))
# Statistic test (NV_1)
NV1 <- (1/sqrt(t_bar))*Nt
# Statistic test (NV_2)
NV2 <- (sqrt(v_theoric)/sqrt(v_empiric))*NV1
# Rejection level 
t_alpha <- qnorm(ci/2)
# =============== Kable =============== 
kab <- dplyr::tibble(
  n = t_bar,
  alpha_hat = paste0(format(sum(vt)/t_bar*100, digits = 3), "%"),
  t_alpha_dw = t_alpha,
  NV1 = NV1,
  NV2 = NV2,
  t_alpha_up = -t_alpha,
  H01 = ifelse(NV1 > t_alpha_up | NV1 < t_alpha_dw, "Rejected", "Non-Rejected"),
  H02 = ifelse(NV2 > t_alpha_up | NV2 < t_alpha_dw, "Rejected", "Non-Rejected")
)  %>%
  dplyr::mutate_if(is.numeric, round, digits = 4)
colnames(kab) <- c("$$n$$", "$$\\frac{N_n}{n}$$", "$$-t_{\\alpha/2}$$", 
                   "$$NV_1$$", "$$NV_2$$", "$$t_{\\alpha/2}$$", "$$H_0(NV_1)$$", "$$H_0(NV_2)$$")
knitr::kable(kab, booktabs = TRUE ,escape = FALSE, align = 'c')%>%
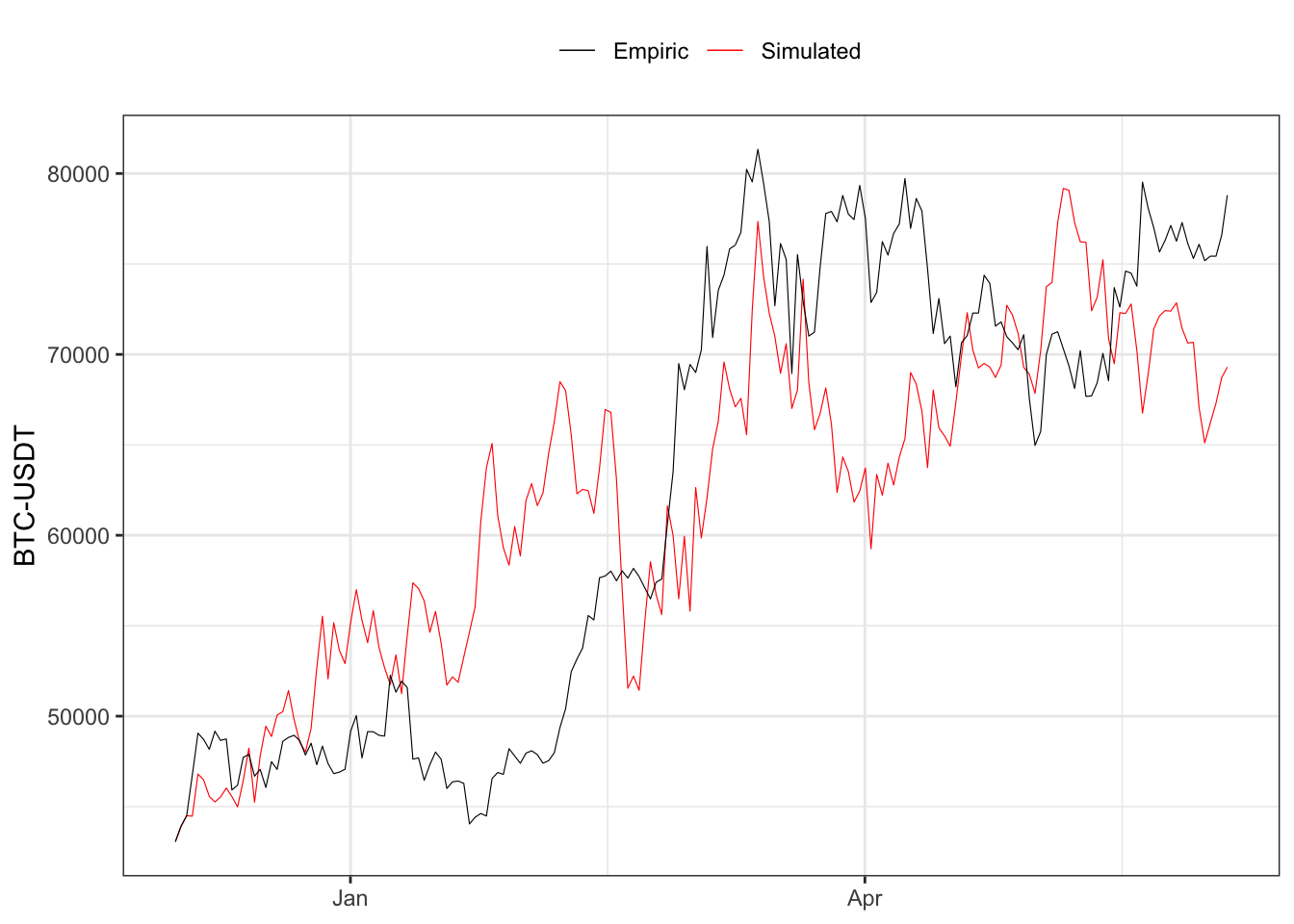
  kableExtra::row_spec(0, color = "white", background = "green") 

Table 4: Test at ${\alpha }^{\ast }=0.05$ on the number of violations of the theoric VaR at $\alpha =0.05$ for log-returns of $\text{BTC}$.

$$n$$	$$\frac{N_n}{n}$$	$$-t_{\alpha /2}$$	$$N{V}_1$$	$$N{V}_2$$	$$t_{\alpha /2}$$	$$H_0(N{V}_1)$$	$$H_0(N{V}_2)$$
2193	4.38%	-1.96	-1.3374	-1.4247	1.96	Non-Rejected	Non-Rejected

# ==================== Setups =====================
set.seed(3959) # random seed 
parAR <- c(mu=0, phi1=0, phi2=0) # AR parameters
parGARCH <- GARCH_model@fit$coef # GARCH parameters
# long-term std deviation of residuals 
sigma_eps <- sqrt(parGARCH[1]/(1-sum(parGARCH[-1])))
# ================== Simulation ===================
# Initial points
Xt <- data_test$Rt
# number of simulations 
t_bar <- length(Xt)
mu <- rep(parAR[1]/(1-sum(parAR[-1])), 4)
sigma <- rep(sigma_eps, 4)
# Simulated residuals 
eps <- rnorm(t_bar) 
eps[1:4] = eps[1:4]*sigma[1]
# Value at Risk
q_alpha = qnorm(ci)
VaR = c(0)
for(t in 4:t_bar){
  # AR component 
  mu[t] <- parAR[1] + parAR[2]*Xt[t-1] + parAR[3]*Xt[t-2]
  # ARCH component 
  sigma[t] <- parGARCH[1] + parGARCH[2]*eps[t-1]^2 + parGARCH[3]*eps[t-2]^2 
  # GARCH component 
  sigma[t] <- sigma[t] + parGARCH[4]*sigma[t-1]^2 + parGARCH[5]*sigma[t-2]^2 + parGARCH[6]*sigma[t-3]^2
  sigma[t] <- sqrt(sigma[t])
  # Simulated residuals 
  eps[t] <- sigma[t]*eps[t]
  # Simulated value at risk
  VaR[t] <- mu[t] + sigma[t]*q_alpha
  # Simulated time series 
  Xt[t] <- mu[t] + eps[t]
}
# Empirical quantile 
q_alpha_emp <- quantile(eps/sigma, probs = ci)
VaR_emp <- mu + sigma*q_alpha_emp

# ===================== Plot ======================
# GARCH(2,3) simulation
ggplot()+
  geom_line(aes(data_test$date, data_test$close[4]*cumprod(exp(Xt)), color = "sim"), size = 0.2)+
  geom_line(aes(data_test$date, data_test$close[4]*cumprod(exp(data_test$Rt)), color = "emp"), size = 0.2)+
  scale_color_manual(values = c(sim = "red", emp = "black"),
                     labels = c(sim = "Simulated", emp = "Empiric"))+
  theme_bw()+
  theme(legend.position = "top")+
  labs(x = NULL, y = "BTC-USDT", color = NULL)

Figure 5: $\text{BTC}$ under GARCH(2,3) model (red) and realized prices (black).