Solar energy
The sun is the main source of renewable energy available on the earth. We define as solar energy every form of energy directly derived from the sun, i.e. the photovoltaic one. However, the other renewable sources are also indirectly connected with the sun. Hydraulic energy, for example, is linked to the water cycle in nature through evaporation and the subsequent precipitation, which is caused by solar heating. Similarly, the winds, from which wind energy derives, are generated by changes in atmospheric pressure linked to solar heating. Finally, also the chemical potential energy of biomass is a form of solar energy storage captured by plants through photosynthesis. From this point of view, it is legitimate to say that fossil fuels also owe their existence to the sun, as they were formed over the geological eras by the anaerobic transformation of organic substances Comini and Savino (2013). It is therefore clear how all the forms of energy that we have at out disposal are directly or indirectly connected to the presence and energy of the sun. This chapter is devoted to understanding the nature of the energy irradiated by the sun and its movements. The first section is devoted to the solar geometry, in which we will go through the definitions of the angles that characterize the position of the sun with respect to a point on the earth and the direction and angle of incidence of a solar solar ray. In the second section we will examine the characteristics of the extraterrestrial radiation: it is important in understanding and using solar radiation data, since it should represent an upper limit of the amount of solar radiation available on the earth. More details on these arguments can be found in Duffie and Beckman (2013).
1 The Sun
The sun is a sphere with a diameter of 1.39 x
However, in reality the sun does not work, as a black body radiator at a fixed temperature, rather the emitted solar radiation is the composite result of the several layers that emit and absorb radiation of various wavelengths. The final extraterrestrial solar radiation and its spectral distribution have now been measured by various methods in several experiments. The solar spectrum changes throughout the day and with location. Standard reference spectra are defined to allow the performance comparison of photovoltaic devices from different manufacturers and research laboratories. We can distinguish between three main standards:
- AM0: is the standard spectrum for space applications, it has an integrated power of
- AM1.5 Global spectrum: is designed for flat plate modules and has an integrated power of
- AM1.5 Direct spectrum: is defined for solar concentrator work, it includes the direct beam from the sun plus the circumsolar component in a disk 2.5 degrees around the sun. The direct plus circumsolar spectrum has an integrated power density of
The data for these three spectra are available for the download at the website2. Assuming that the sun behaves as a blackbody, we could compare these spectra with the theoretical distribution obtained by the Planck’s law. Denoting as
In Equation 1,
As consequence
1.1 Radiation Definitions
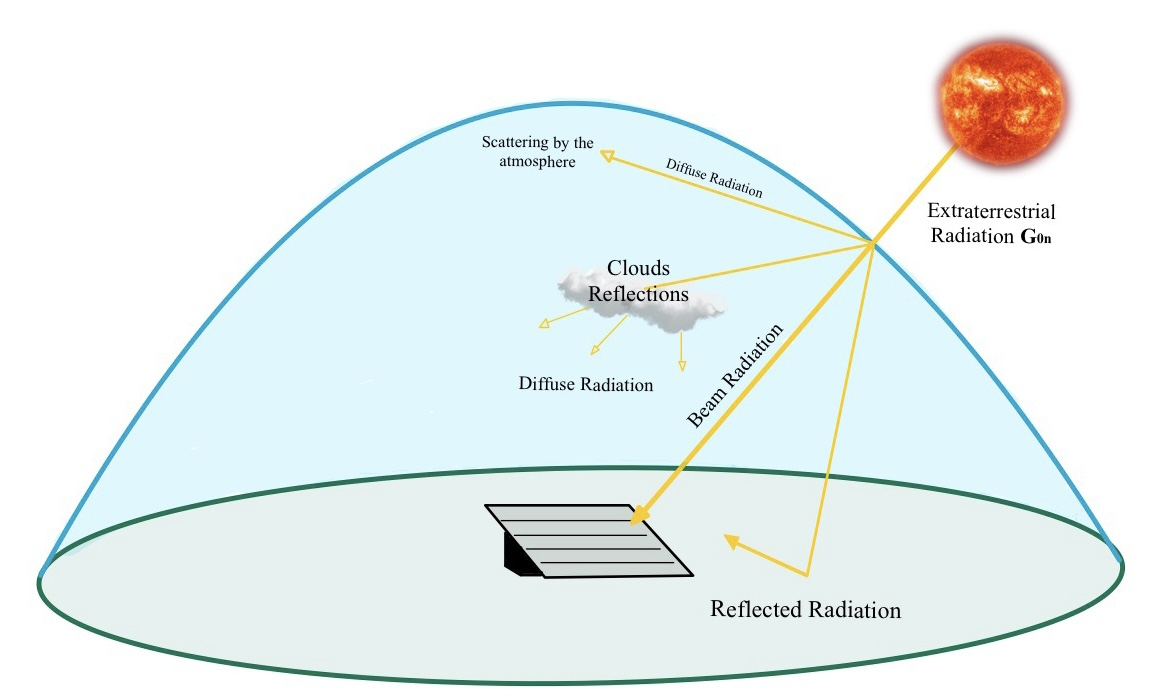
As the solar radiation goes through the atmosphere it suffers different processes of absorption, dispersion or scattering that result in lower levels of solar radiation being received at the Earth’s surface. These are due to the atmosphere components, such as ozone or
Extraterrestrial Radiation: it represents the amount of radiation that could be theoretically available if there were no atmosphere. Even if it could present some randomness, in general it is considered deterministic. Once the radiation enters in the atmosphere we could make two further distinctions in beam and diffuse radiation. The notations involved are several:
Beam Radiation: it represents the solar radiation received from the sun without being scattered by the atmosphere. Consequently to its definition, the Beam radiation is maximum when the sky is clear3. In theory the Beam radiation can be zero: even if this could seem strange, in days when the sky is fully covered by clouds, the instruments devoted to the measurement4 could register a value of zero. It is also denoted as Direct Normal Irradiance or DNI.
Diffuse Radiation: it represents the solar radiation received from the sun after its direction has been changed and scattered by the atmosphere. In application, usually, this measure is considered with respect to an horizontal surface (Diffuse Horizontal Irradiance or DHI).
Global Solar Radiation: it represents the sum of the beam and the diffuse radiations. A common practice is to consider it with respect to an horizontal surface (Global Horizontal Irradiance or GHI).
1.2 Solar constant
The solar constant
However,
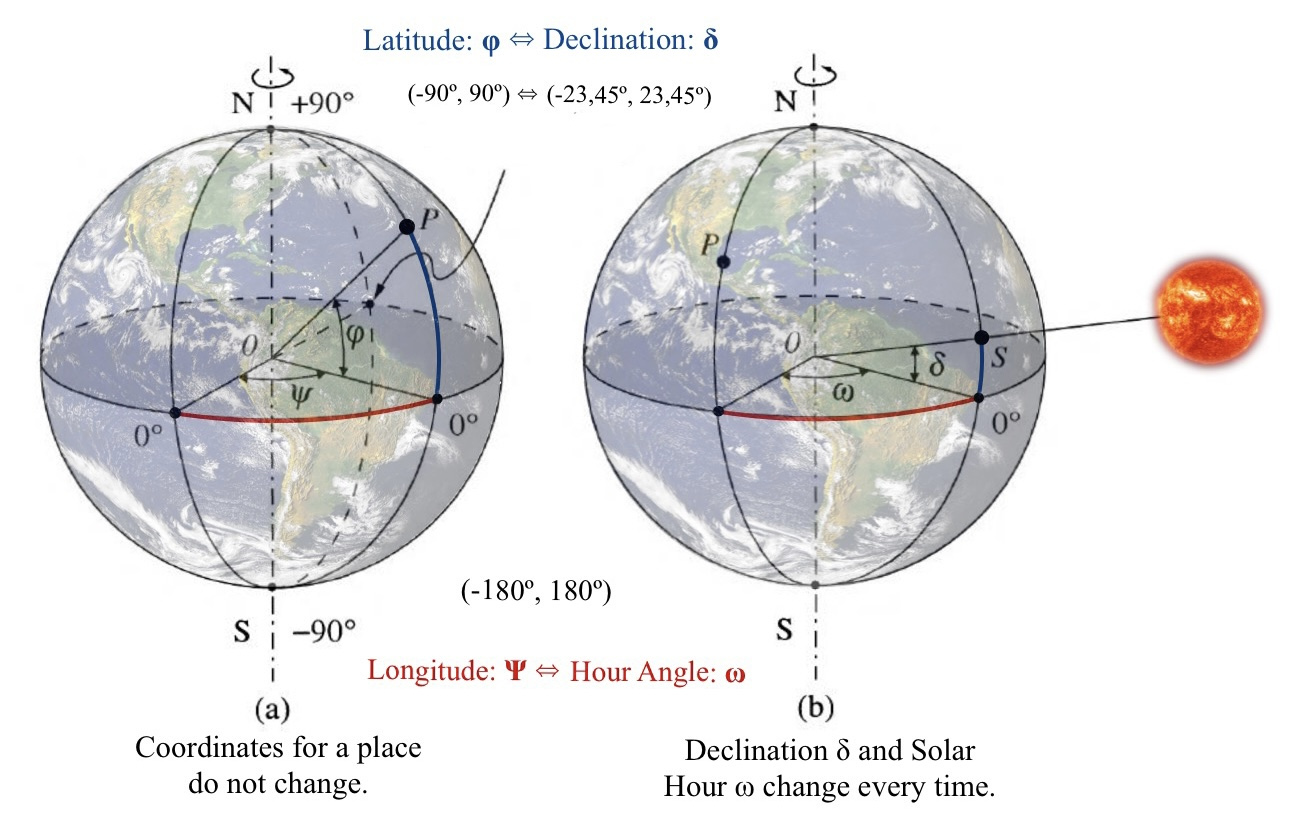
1.3 Equatorial coordinates
The position of the sun with respect to a point
- Latitude
- Longitude
- Solar Declination
- Hour Angle
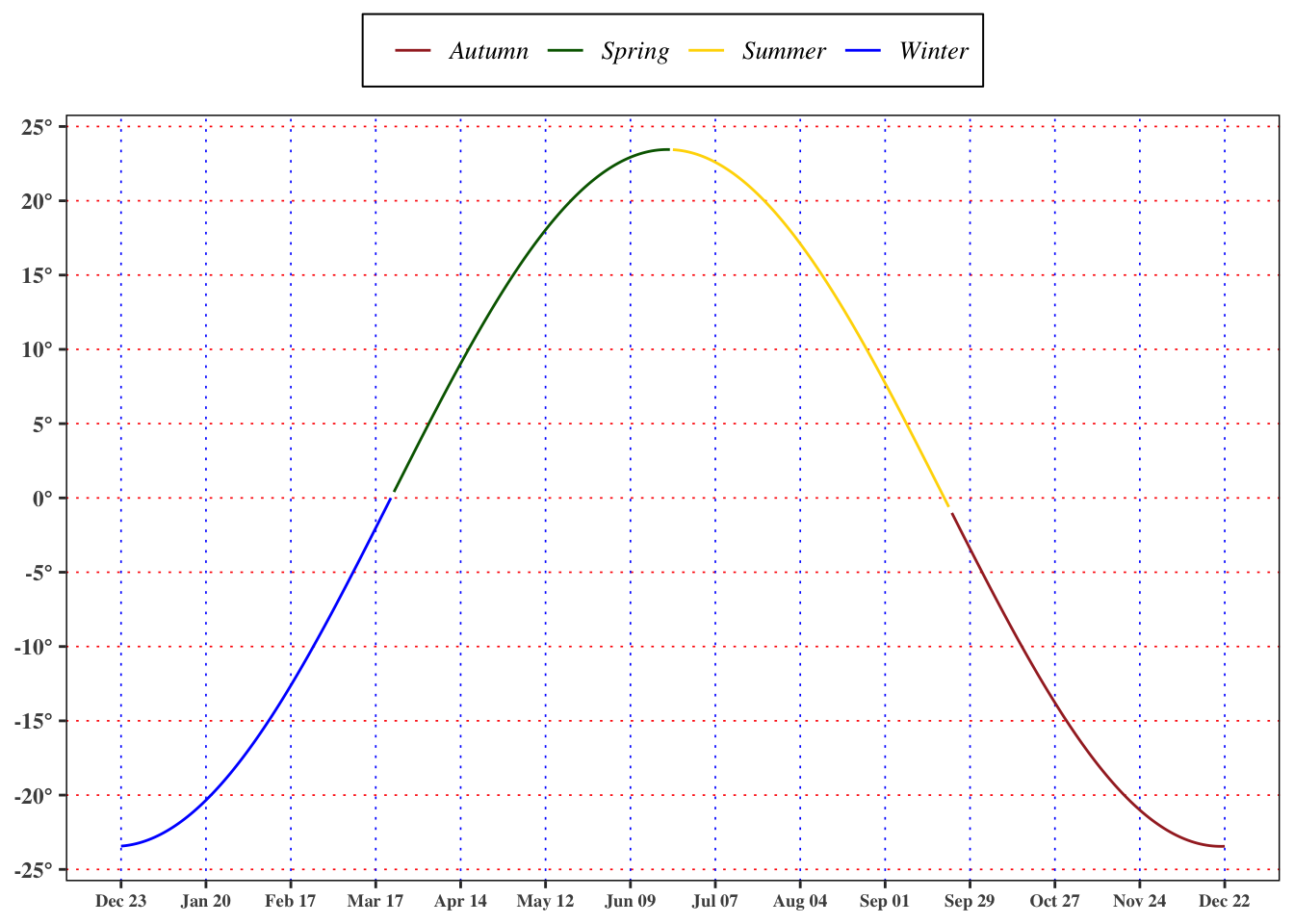
1.3.1 Solar declination
Given
In 1971, Spencer, as cited by Iqbal (1983), found a more accurate specification, that gives an error less
where
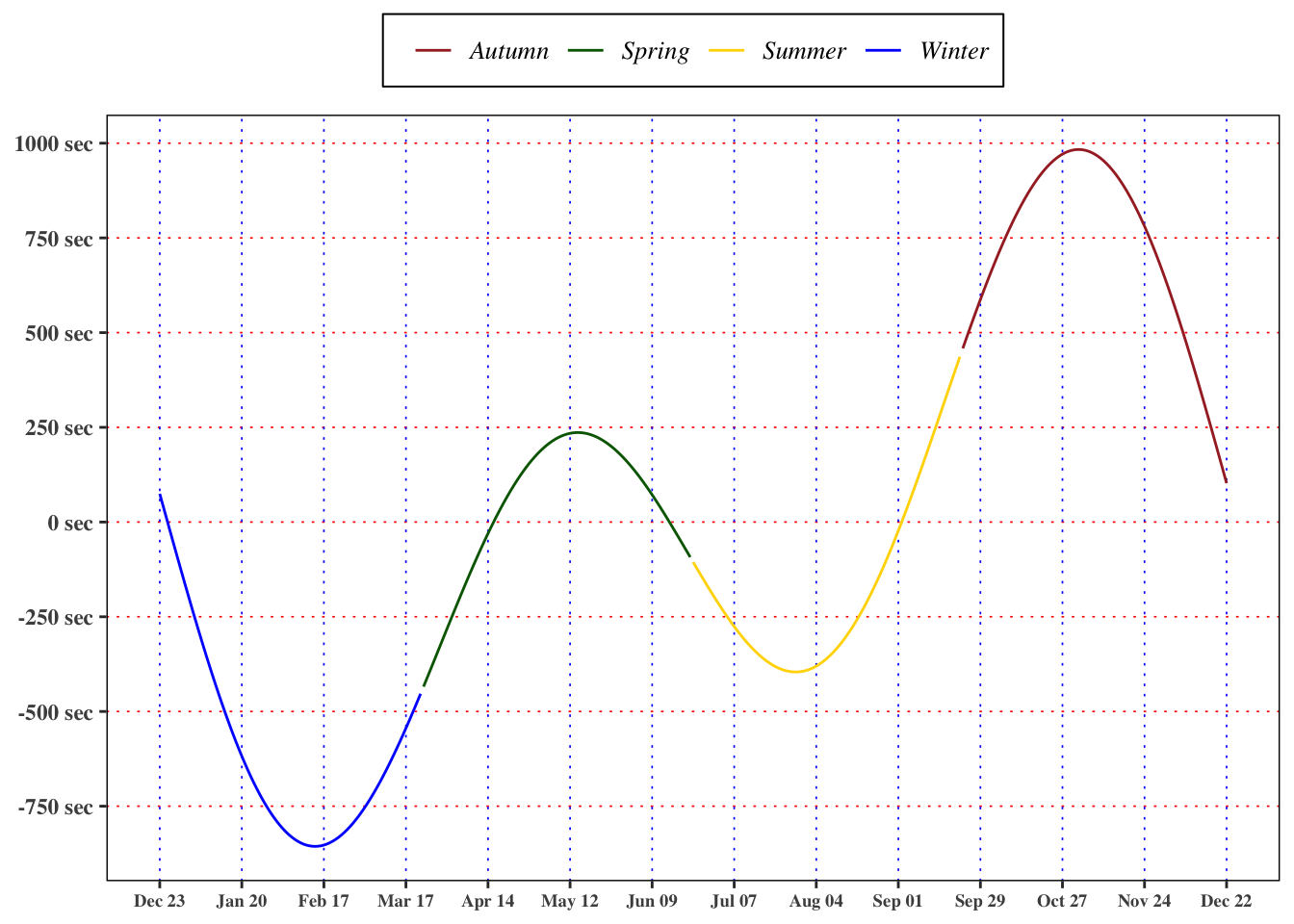
1.3.2 Hour angle
During a movement of rotation of the Earth around its axes the hour angle
where
1.4 Terrestial Coordinates
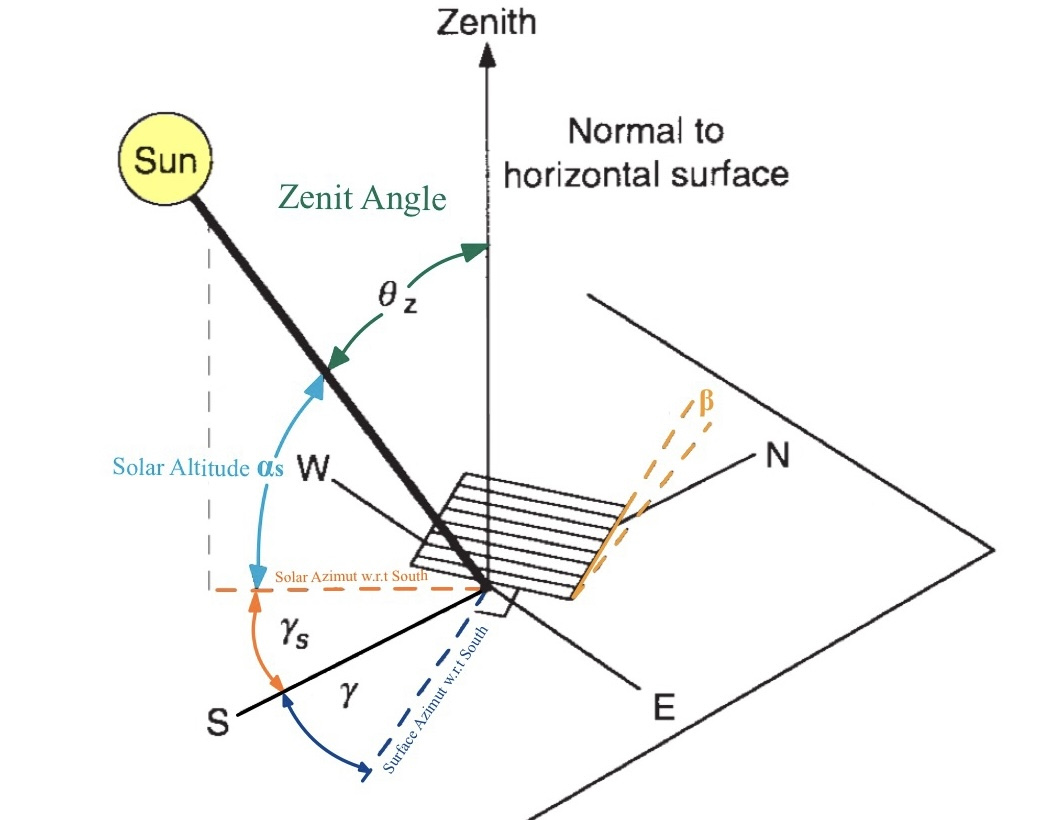
The irradiance of a receiving surface depends on the cosine of the angle of incidence, i.e. the angle that the direction of the sunrays forms with the normal
- Zenith angle
- Solar altitude angle
- Solar azimut angle
- Angle of incidence
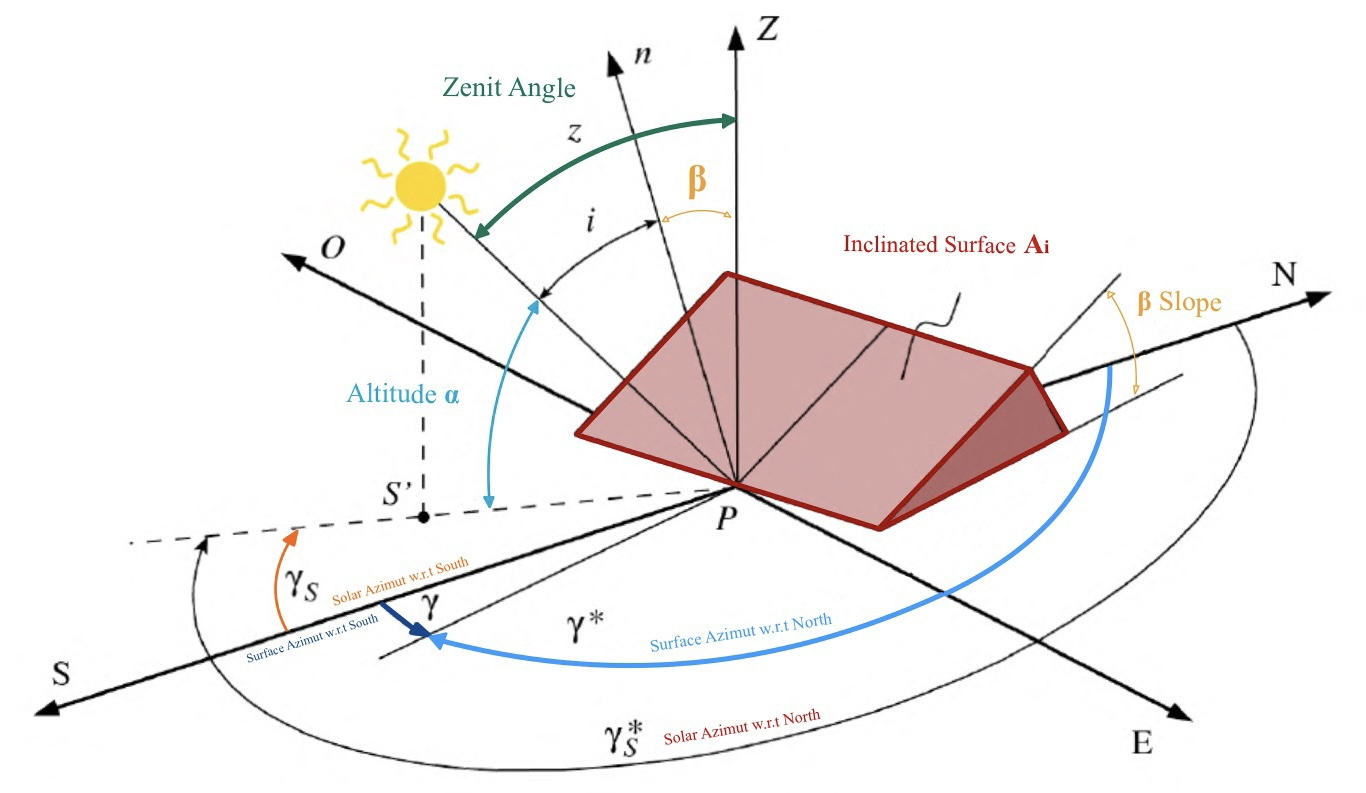
- Slope
- Angle of incidence
- Surface azimut angle
There is a set of relations that connect the angle of incidence to the others that are time varying:
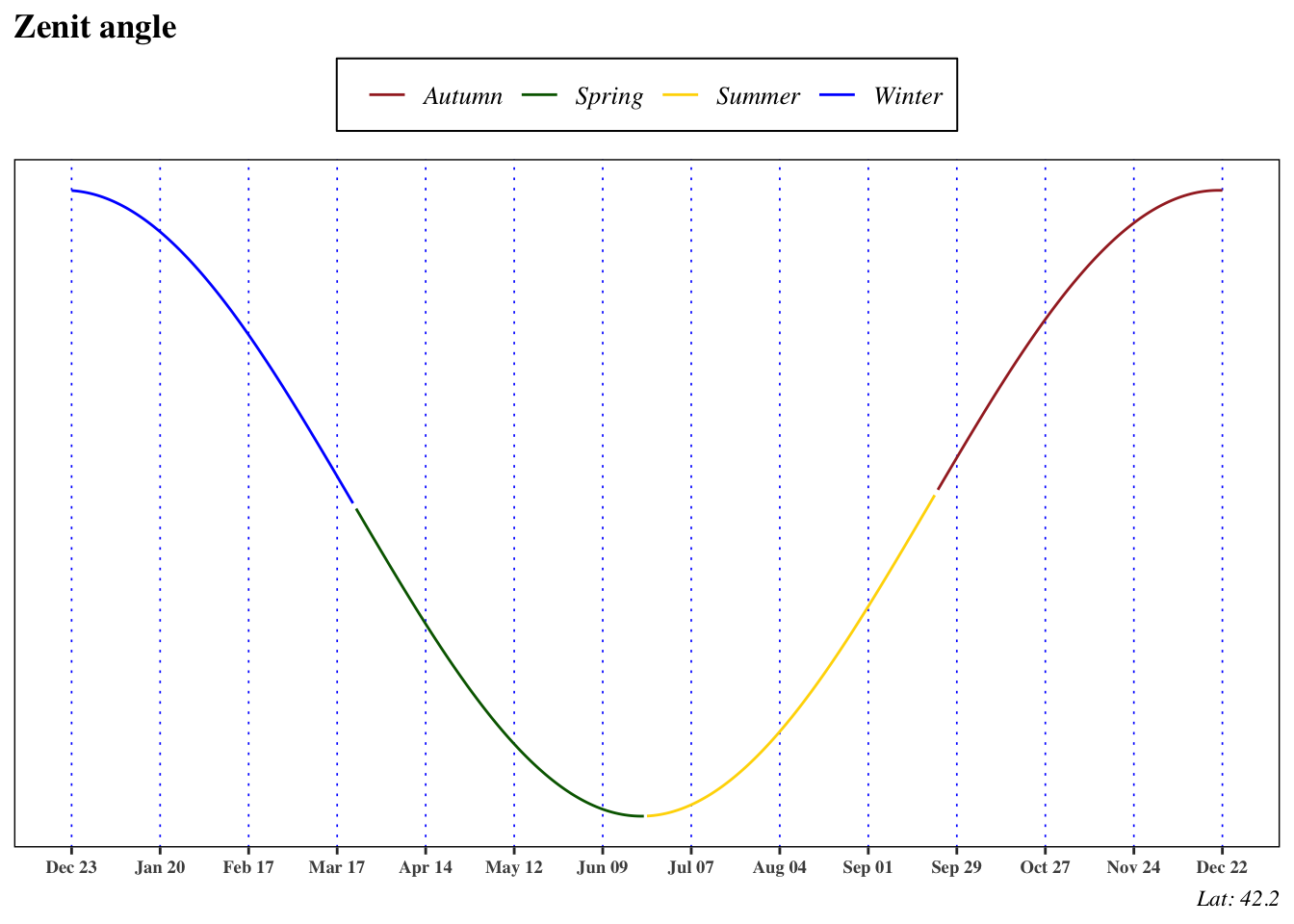
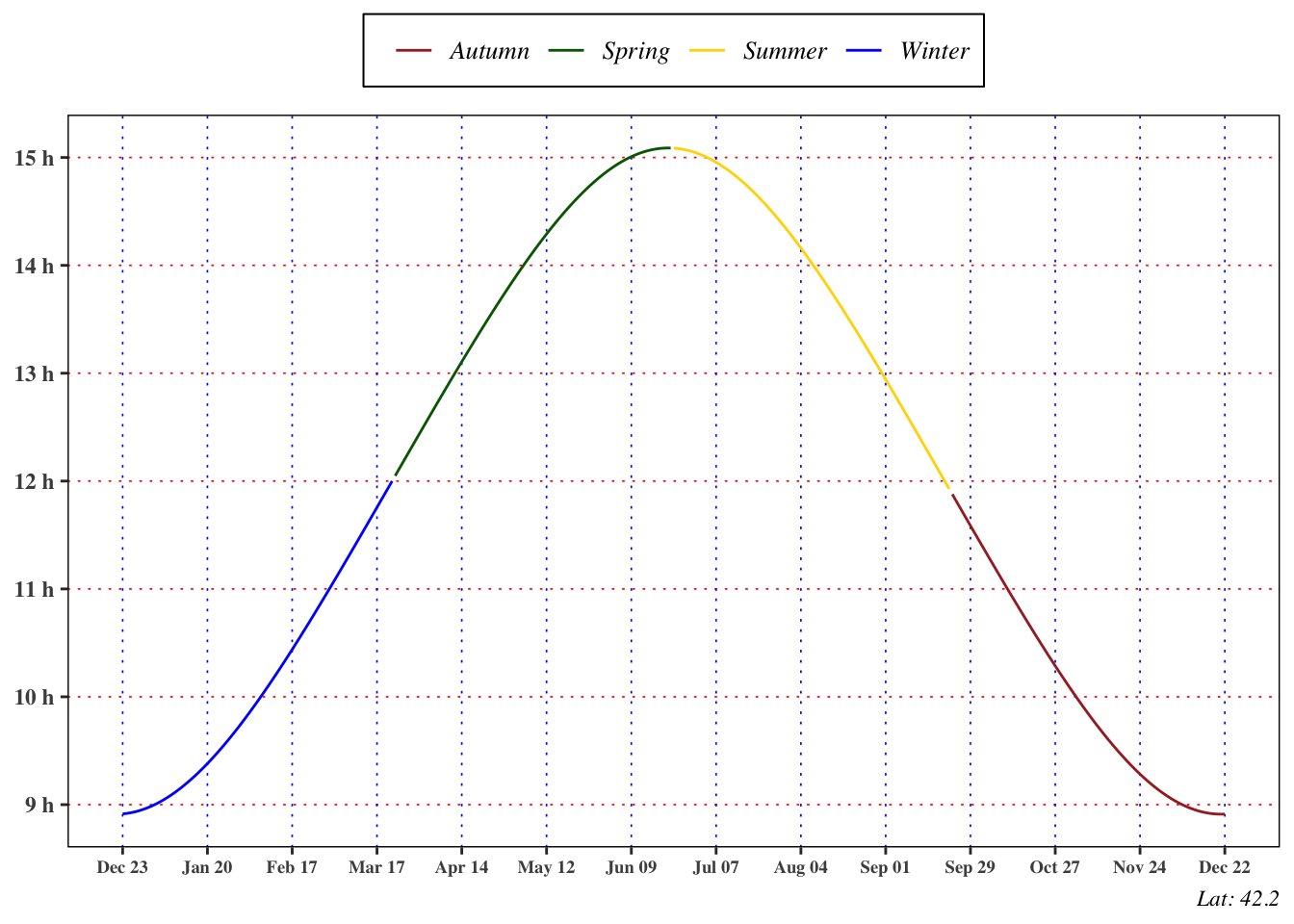
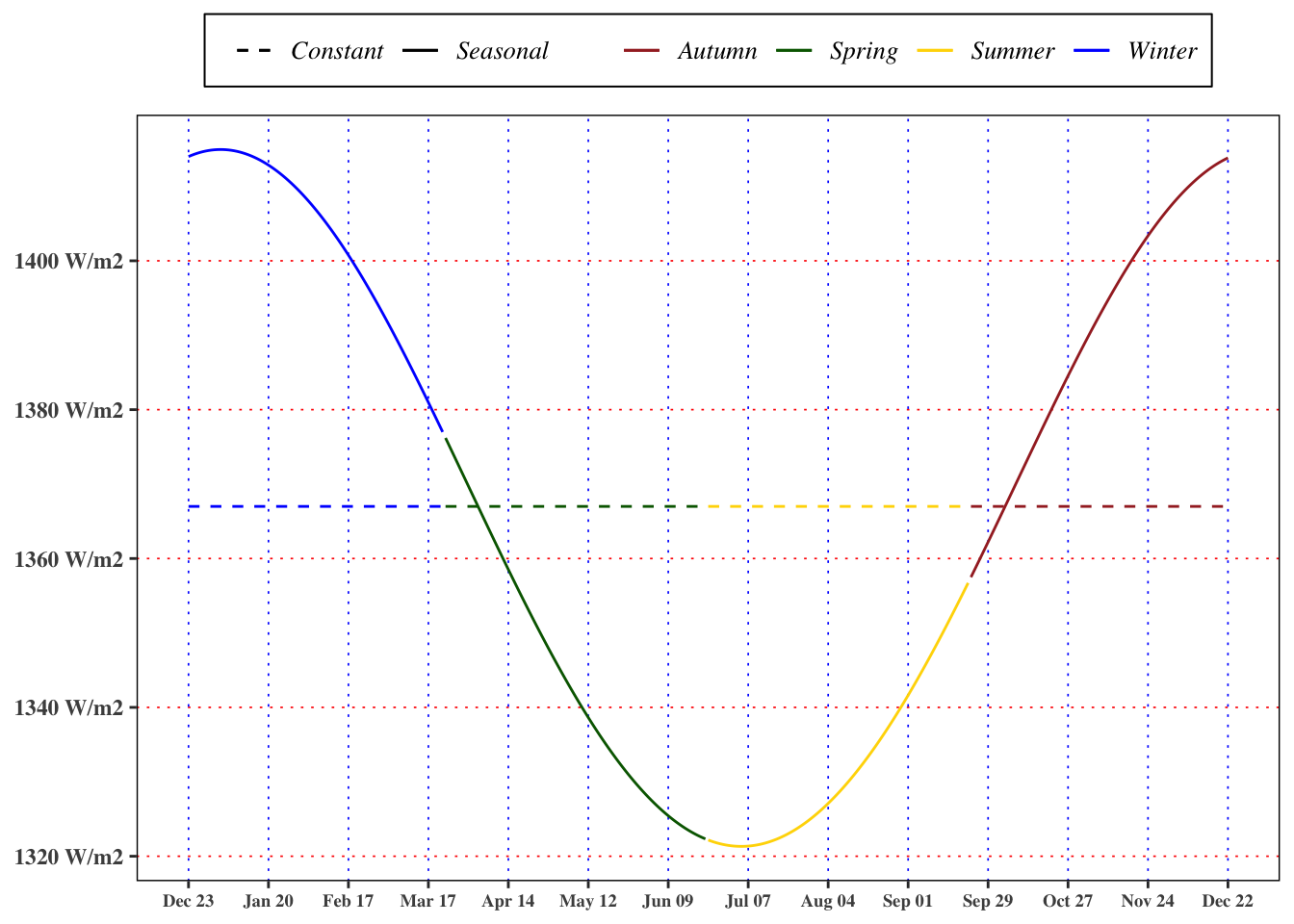
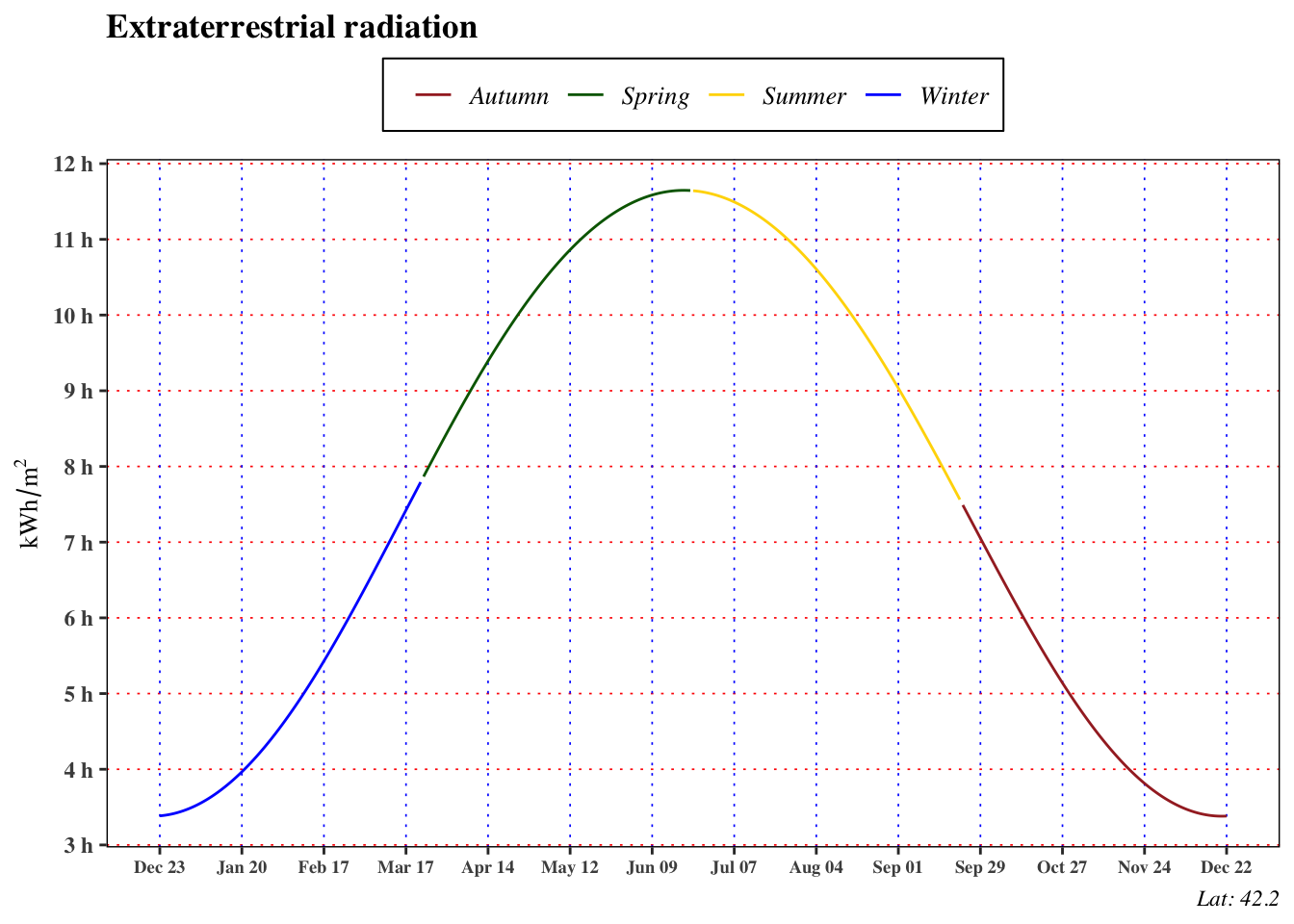
1.5 Extraterrestrial Radiation
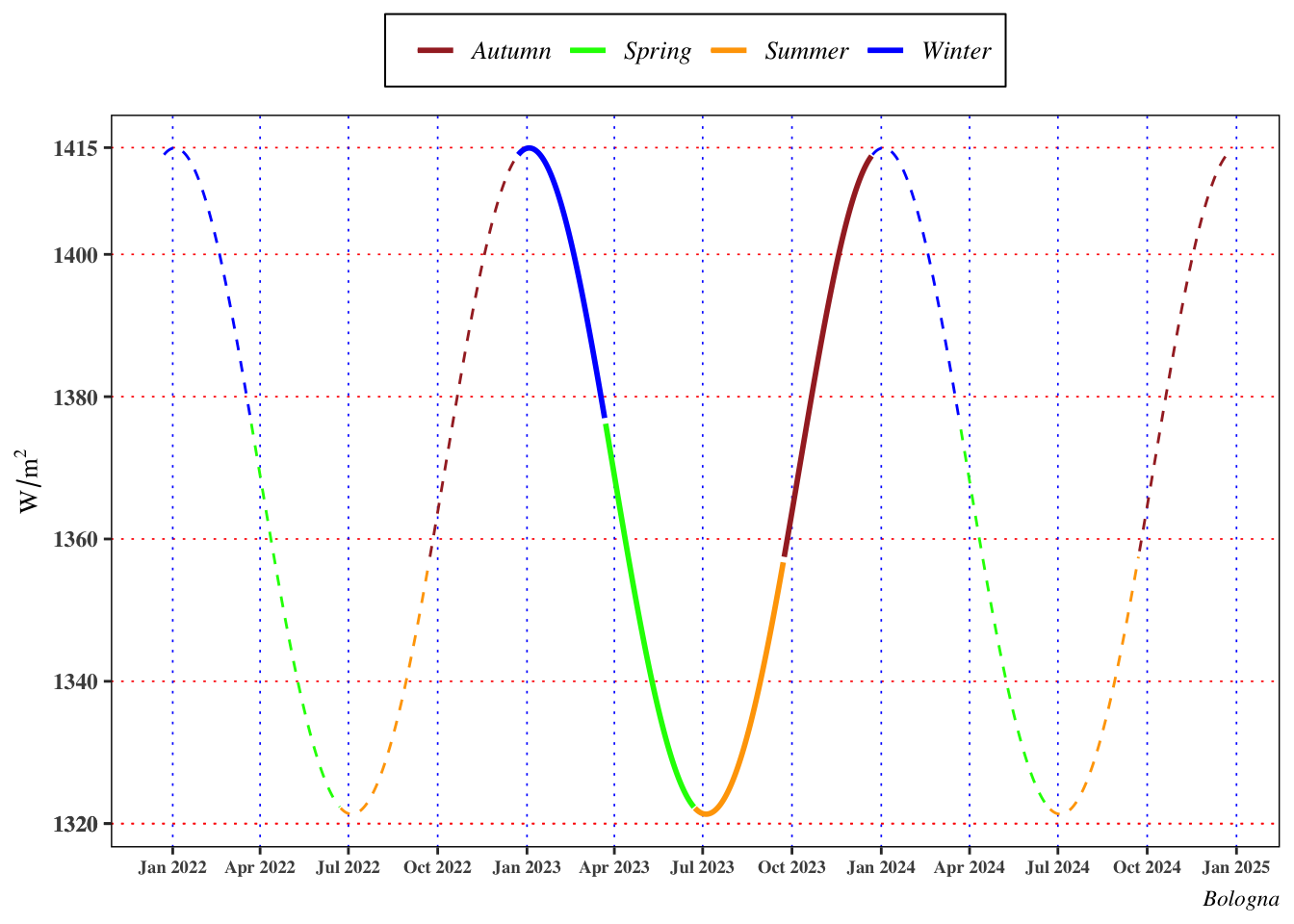
Considering the variation of the extraterrestrial radiation during the year, there are two sources of stochasticity. The first is given by a variation of the radiation emitted by the sun, in literature there are conflicting reports on periodic variations of intrinsic solar radiation. For engineering and modelling purposes this source of stochasticity is neglected. However the second source of variability is given by the different earth-sun distance during the year that leads to difference of
This expression represents the extraterrestrial energy that arrives on an horizontal surface in any time between the sunrise and the sunset. A more useful expression in the application is the daily extraterrestrial horizontal irradiance, denoted as $ H_{n}^{extra}$, that can be computed integrating the formula Equation 14 with respect to
References
Footnotes
The effective black body temperature of 5777 K is the temperature of a black body radiating the same amount of energy as does the sun.↩︎
https://www.nrel.gov/grid/solar-resource/spectra-am1.5.html↩︎
Clear sky is the condition where the visibility is greater or equal to 23km.↩︎
Pyrheliometers are used for the measure of Beam normal radiation, while pyrometers are used for the measure of the global radiation on horizontal surface↩︎
Areas of the sun where the temperature is about 5000 K.↩︎
As is known, the Earth’s axis intersects orthogonally the equatorial plane at the point O, center of the Earth.↩︎
Terrestrial coordinates are centered on a ground surface containing the location P of the observer.↩︎
i.e., the position of the sun relative to that plane↩︎
For Europe the time occurred to move one degree is around 15 minutes.↩︎
Citation
@online{sartini2024,
author = {Sartini, Beniamino},
title = {Solar Energy},
date = {2024-05-01},
url = {https://greenfin.it/solar/solar-energy.html},
langid = {en}
}