ARCH-GARCH process

Author

Affiliation

Beniamino Sartini

University of Bologna

Published

May 1, 2024

Modified

June 16, 2024

Setup

# required for figures  
library(ggplot2)
library(gridExtra)
# required for render latex 
library(backports)
library(latex2exp)

1 ARCH(p) process

The autoregressive conditional heteroskedasticity (ARCH) models were introduced in 1982 by Robert Engle to model varying (conditional) variance of time series. It is often found in economics that the larger values of time series also lead to larger instability. Let’s define a time series such as $X_{t} \sim A R C H (p)$ , then it is defined as: $\begin{aligned} x_{t} = μ + e_{t} \\ e_{t} = σ_{t} u_{t} \\ σ_{t}^{2} = ω + \sum_{i = 1}^{p} α_{i} e_{t - i}^{2} \end{aligned}$ where $u_{t} \sim MDS (0, 1)$ .

Tip 1: Stationary ARCH(p)

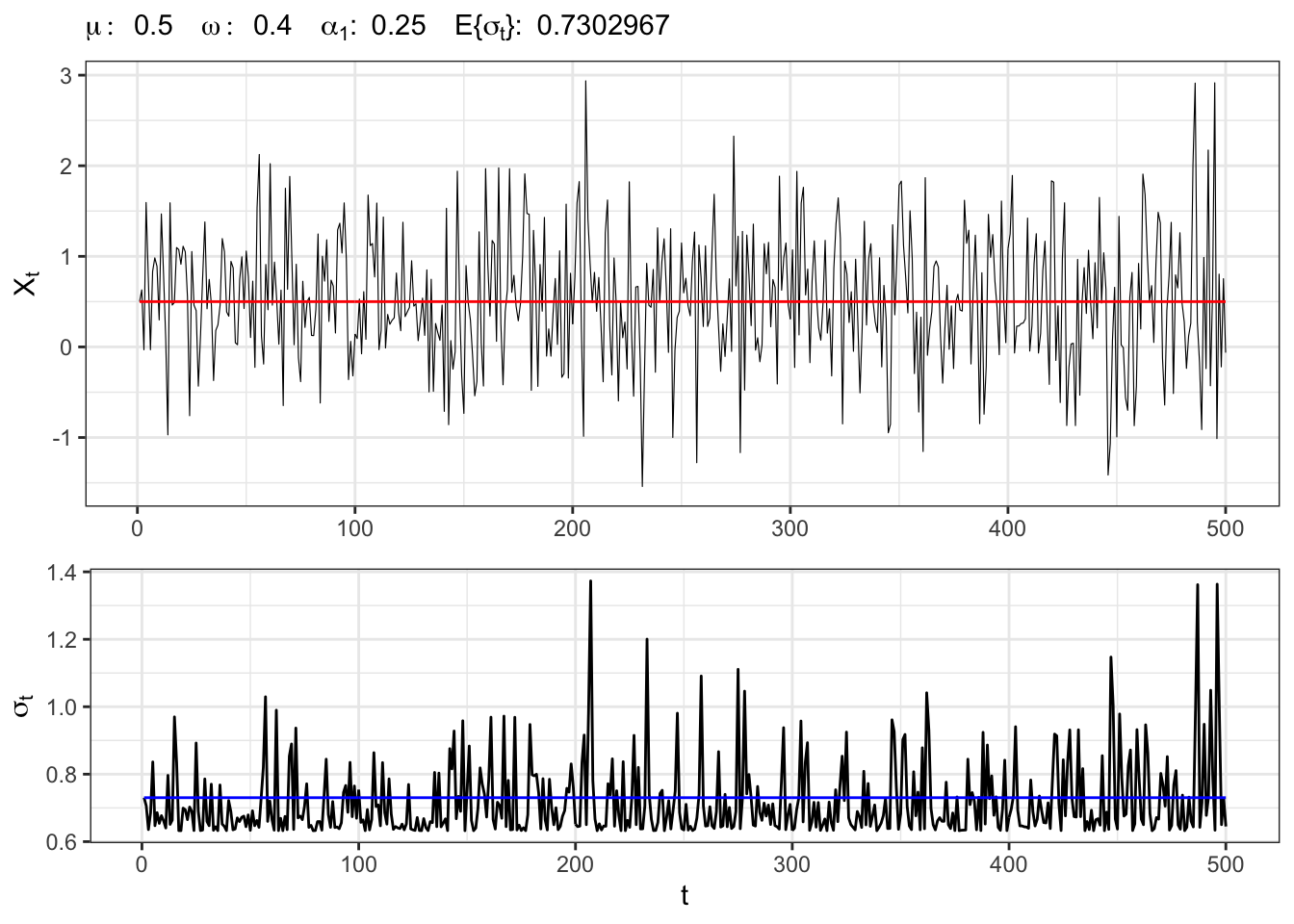
The unconditional and conditional mean of a process $X_{t} \sim A R C H (p)$ are equal to: $E {X_{t}} = E {X_{t} | I_{t - 1}} = μ,$ where $I_{t - 1}$ denotes the information available up to time $t - 1$ . Instead, the long term variance of the process, i.e. the unconditional variance, is defined as: $\begin{aligned} V {X_{t}} & = V {μ + σ_{t} u_{t}} = \\ = V {σ_{t} u_{t}} = & (E {u_{t}} = 0) \\ = E {σ_{t}^{2} u_{t}^{2}} = & (u_{t} iid) \\ = E {σ_{t}^{2}} E {u_{t}^{2}} = & (E {u_{t}^{2}} = 1) \\ = E {σ_{t}^{2}} \cdot 1 \end{aligned}$ where the unconditional expectation of the stochastic variance is given by $E {σ_{t}^{2}} = \frac{ω}{1 - \sum_{i = 1}^{p} α_{i}} .$ It is clear that, in general $ω \neq 0$ and, to ensure that the process is stationary, the following condition on the parameters must be satisfied: $\sum_{i = 1}^{p} α_{i} < 1 α_{i} > 0 \forall i$

1.1 Example: ARCH(1) process

Let’s simulate an ARCH(1) process with normal residuals, namely $X_{t} \sim A R C H (1)$ , i.e. $\begin{aligned} x_{t} = μ + e_{t} \\ e_{t} = σ_{t} u_{t} \\ σ_{t}^{2} = ω + α_{1} e_{t - 1}^{2} \end{aligned}$ where $u_{t} \sim N (0, 1)$ .

ARCH(1) simulation

# Random seed 
set.seed(1)
# ==================== Setups =====================
# Nsumber of simulations 
t_bar <- 500 
# Parameters
par <- c(mu=0.5, omega=0.4, alpha1=0.25) 
# Long-term std deviation of residuals 
sigma_eps <- sqrt(par[2]/(1-par[3]))
# ================== Simulation ===================
# Initial point
Xt <- rep(par[1], 1)
# Store stochastic variance 
sigma <- rep(sigma_eps, 1)
# Simulated residuals 
eps <- rnorm(t_bar, 0, 1) 
for(t in 2:t_bar){
  # ARCH(1) variance 
  sigma[t] <- par[3]*eps[t-1]^2
  # ARCH(1) std. deviation 
  sigma[t] <- sqrt(par[2] + sigma[t])
  # Simulated residuals 
  eps[t] <- sigma[t]*eps[t]
  # Simulated time series 
  Xt[t] <- par[1] + eps[t]
}
# ===================== Plot ======================
# ARCH(1) simulation
plot_arch <- ggplot()+
  geom_line(aes(1:t_bar, Xt), size = 0.2)+
  geom_line(aes(1:t_bar, par[1]), color = "red")+
  theme_bw()+
  labs(x = NULL, y = TeX("$X_t$"),
       subtitle = TeX(paste0("$\\mu:\\;", par[1], 
                             "\\;\\; \\omega:\\;", par[2], 
                             "\\;\\; \\alpha_{1}:\\;", par[3],
                             "\\;\\; E\\{\\sigma_t\\}:\\;", sigma_eps,
                             "$")))
# ARCH(1) std. deviation
plot_sigma <- ggplot()+
  geom_line(aes(1:t_bar, sigma), alpha = 1)+
  geom_line(aes(1:t_bar, sigma_eps), alpha = 1, color = "blue")+
  labs(x = "t", y = TeX("$\\sigma_{t}$"))+
  theme_bw()
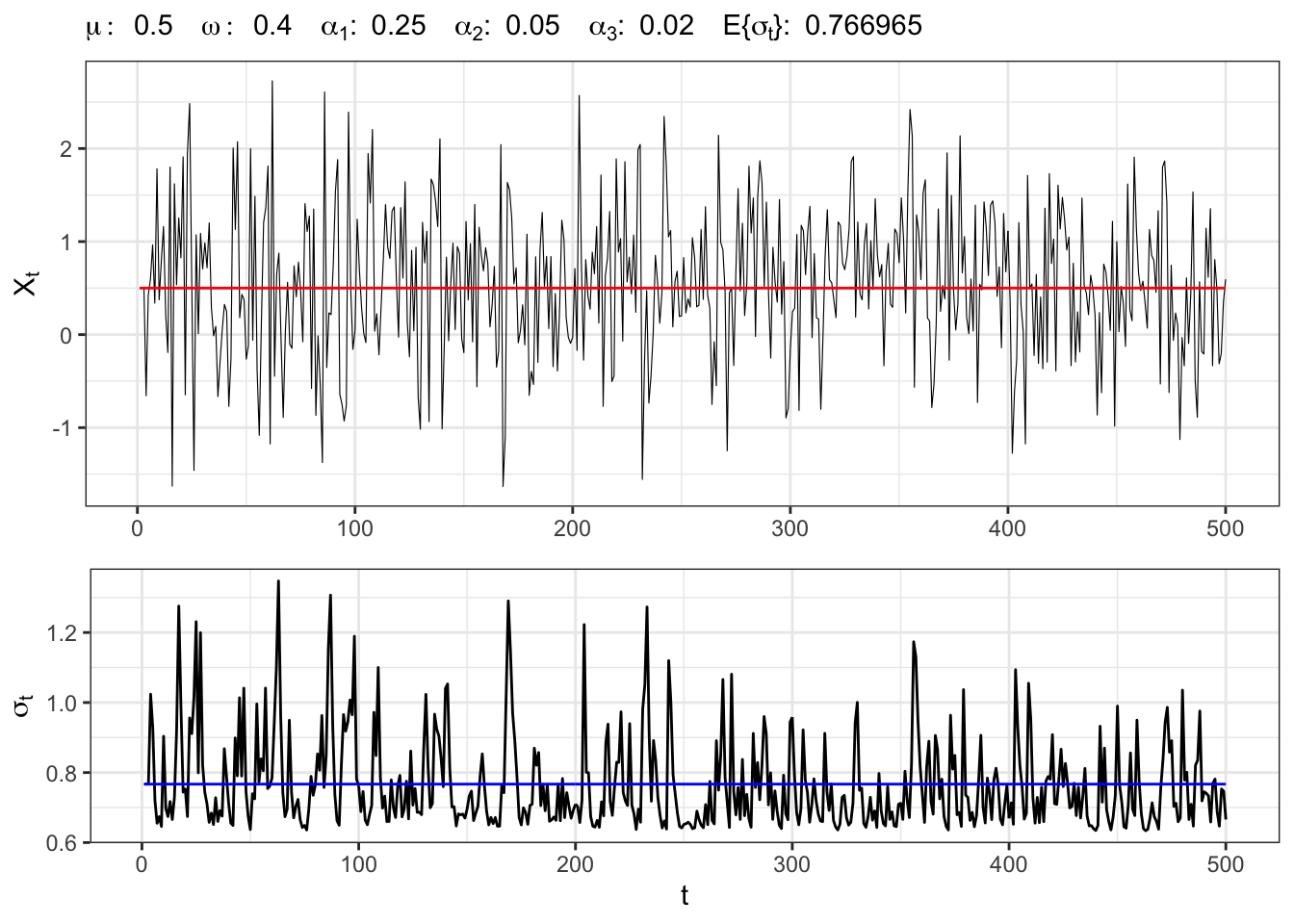
gridExtra::grid.arrange(plot_arch, plot_sigma, heights = c(0.6, 0.4))

1.2 Example: ARCH(3) process

Let’s simulate an ARCH(3) process with normal residuals, namely $X_{t} \sim A R C H (3)$ , i.e. $\begin{aligned} x_{t} = μ + e_{t} \\ e_{t} = σ_{t} u_{t} \\ σ_{t}^{2} = ω + α_{1} e_{t - 1}^{2} + α_{2} e_{t - 2}^{2} + α_{3} e_{t - 3}^{2} \end{aligned}$ where $u_{t} \sim N (0, 1)$ .

ARCH(3) simulation

# Random seed 
set.seed(2)
# ==================== Setups =====================
# Number of simulations 
t_bar <- 500 
# Parameters
par <- c(mu=0.5, omega=0.4, 
         alpha1=0.25, alpha2=0.05,alpha3=0.02) 
# Long-term std deviation of residuals 
sigma_eps <- sqrt(par[2]/(1-sum(par[3:5])))
# ================== Simulation ===================
# Initial point
Xt <- rep(par[1], 3)
# Store stochastic variance 
sigma <- rep(sigma_eps, 3)
# Simulated residuals 
eps <- rnorm(t_bar, 0, 1) 
for(t in 4:t_bar){
  # ARCH(3) variance 
  sigma[t] <- par[3]*eps[t-1]^2 + par[4]*eps[t-2]^2 + par[5]*eps[t-3]^2
  # ARCH(3) std. deviation 
  sigma[t] <- sqrt(par[2] + sigma[t])
  # Simulated residuals 
  eps[t] <- sigma[t]*eps[t]
  # Simulated time series 
  Xt[t] <- par[1] + eps[t]
}
# ===================== Plot ======================
# ARCH(3) simulation
plot_arch <- ggplot()+
  geom_line(aes(1:t_bar, Xt), size = 0.2)+
  geom_line(aes(1:t_bar, par[1]), color = "red")+
  theme_bw()+
  labs(x = NULL, y = TeX("$X_t$"),
       subtitle = TeX(paste0("$\\mu:\\;", par[1], 
                             "\\;\\; \\omega:\\;", par[2], 
                             "\\;\\; \\alpha_{1}:\\;", par[3],
                             "\\;\\; \\alpha_{2}:\\;", par[4],
                             "\\;\\; \\alpha_{3}:\\;", par[5],
                             "\\;\\; E\\{\\sigma_t\\}:\\;", sigma_eps,
                             "$")))
# ARCH(3) std. deviation
plot_sigma <- ggplot()+
  geom_line(aes(1:t_bar, sigma), alpha = 1)+
  geom_line(aes(1:t_bar, sigma_eps), alpha = 1, color = "blue")+
  labs(x = "t", y = TeX("$\\sigma_{t}$"))+
  theme_bw()
gridExtra::grid.arrange(plot_arch, plot_sigma, heights = c(0.6, 0.4))

2 GARCH(p,q) process

As done with the ARCH(p), with generalized autoregressive conditional heteroskedasticity (GARCH) we model the dependency of the conditional second moment. It represents a more parsimonious way to express the conditional variance. Let’s consider a process $X_{t} \sim GARCH (p, q)$ , then it is defined as: $\begin{aligned} x_{t} = μ + e_{t} \\ e_{t} = σ_{t} u_{t} \\ σ_{t}^{2} = ω + \sum_{i = 1}^{p} α_{i} e_{t - i}^{2} + \sum_{j = 1}^{q} β_{j} σ_{t - j}^{2} \end{aligned}$ where $u_{t} \sim MDS (0, 1)$ .

Tip 2: Stationary GARCH(p,q)

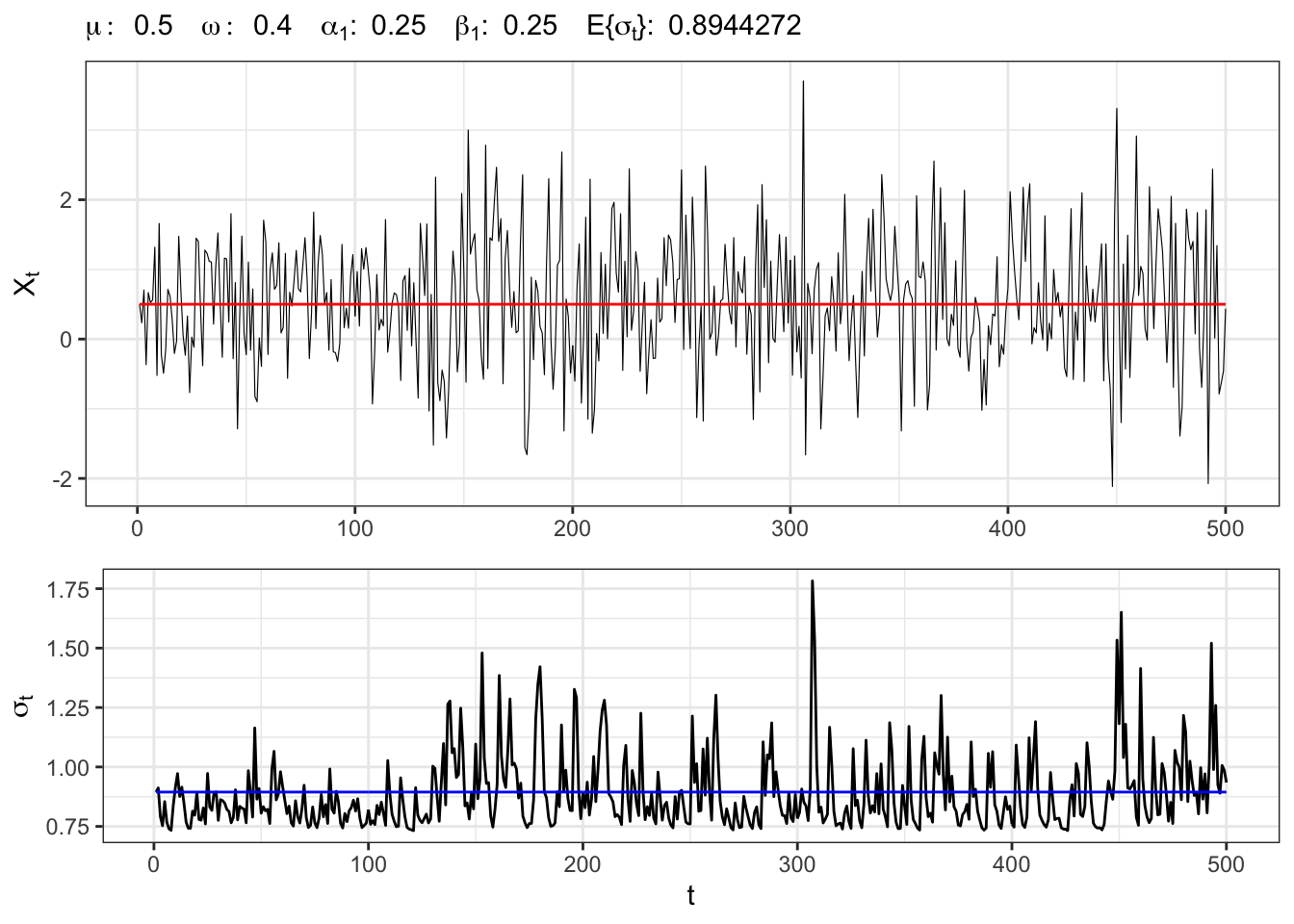
The unconditional and conditional mean of a process $X_{t} \sim G A R C H (p, q)$ are equal to: $E {X_{t}} = E {X_{t} | I_{t - 1}} = μ,$ where $I_{t - 1}$ denotes the information available up to time $t - 1$ . Instead, the long term variance of the process, i.e. the unconditional variance, is defined as for the ARCH(p) model:
$V {X_{t}} = E {σ_{t}^{2}}$ where what changes is the unconditional expectation of the stochastic variance i.e. $E {σ_{t}^{2}} = \frac{ω}{1 - \sum_{i = 1}^{p} α_{i} - \sum_{j = 1}^{q} β_{j}} .$ It is clear that, in general $ω \neq 0$ and, to ensure that the process is stationary, the following condition on the parameters must be satisfied: $\sum_{i = 1}^{p} α_{i} + \sum_{j = 1}^{q} β_{j} < 1 α_{i}, β_{j} > 0 \forall i, \forall j .$

2.1 Example: GARCH(1,1) process

Let’s simulate an GARCH(1,1) process with normal residuals, namely $X_{t} \sim G A R C H (1, 1)$ , i.e. $\begin{aligned} x_{t} = μ + e_{t} \\ e_{t} = σ_{t} u_{t} \\ σ_{t}^{2} = ω + α_{1} e_{t - 1}^{2} + β_{1} σ_{t - 1}^{2} \end{aligned}$ where $u_{t} \sim N (0, 1)$ .

GARCH(1,1) simulation

# Random seed 
set.seed(3)
# ==================== Setups =====================
# number of simulations 
t_bar <- 500 
# parameters
par <- c(mu=0.5, omega=0.4, alpha1=0.25, beta1=0.25) 
# long-term std deviation of residuals 
sigma_eps <- sqrt(par[2]/(1 - par[3] - par[4]))
# ================== Simulation ===================
# Initial points
Xt <- rep(par[1], 1)
sigma <- rep(sigma_eps, 1)
# Simulated residuals 
eps <- rnorm(t_bar, 0, 1) 
for(t in 2:t_bar){
  # GARCH(1,1) variance 
  sigma[t] <- par[3]*eps[t-1]^2 + par[4]*sigma[t-1]^2
  # GARCH std. deviation 
  sigma[t] <- sqrt(par[2] + sigma[t])
  # Simulated residuals 
  eps[t] <- sigma[t]*eps[t]
  # Simulated time series 
  Xt[t] <- par[1] + eps[t]
}
# ===================== Plot ======================
# GARCH(1,1) simulation
plot_garch <- ggplot()+
  geom_line(aes(1:t_bar, Xt), size = 0.2)+
  geom_line(aes(1:t_bar, par[1]), color = "red")+
  theme_bw()+
  labs(x = NULL, y = TeX("$X_t$"),
       subtitle = TeX(paste0("$\\mu:\\;", par[1], 
                             "\\;\\; \\omega:\\;", par[2], 
                             "\\;\\; \\alpha_{1}:\\;", par[3],
                             "\\;\\; \\beta_{1}:\\;", par[4],
                             "\\;\\; E\\{\\sigma_t\\}:\\;", sigma_eps,
                             "$")))
# GARCH(1,1) std. deviation
plot_sigma <- ggplot()+
  geom_line(aes(1:t_bar, sigma), alpha = 1)+
  geom_line(aes(1:t_bar, sigma_eps), alpha = 1, color = "blue")+
  labs(x = "t", y = TeX("$\\sigma_{t}$"))+
  theme_bw()
gridExtra::grid.arrange(plot_garch, plot_sigma, heights = c(0.6, 0.4))

2.2 Example: GARCH(2,3) process

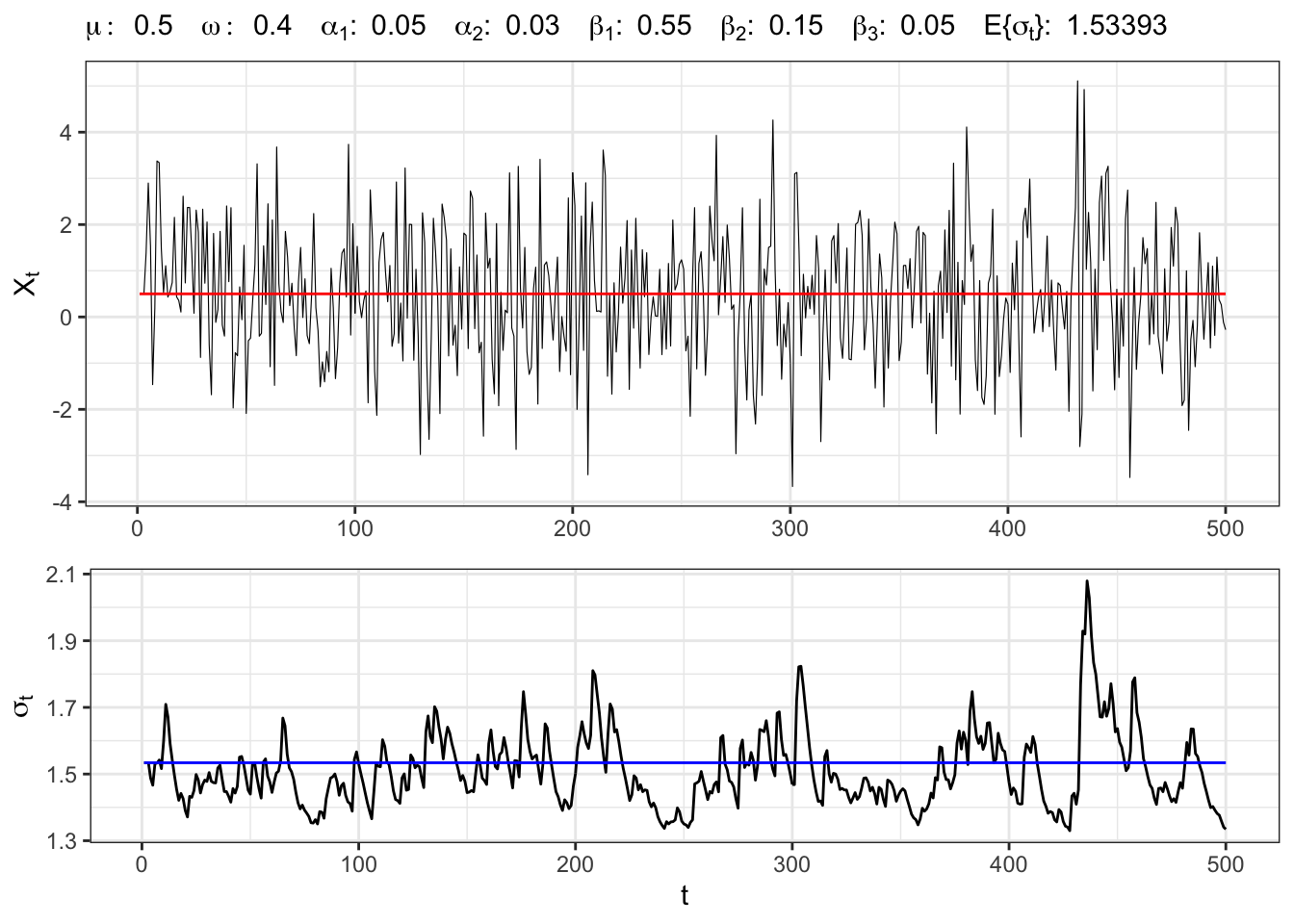
Let’s simulate an GARCH(2,3) process with normal residuals, namely $X_{t} \sim G A R C H (2, 3)$ , i.e. $\begin{aligned} x_{t} = μ + e_{t} \\ e_{t} = σ_{t} u_{t} \\ σ_{t}^{2} = ω + \sum_{i = 1}^{2} α_{i} e_{t - i}^{2} + \sum_{j = 1}^{3} β_{j} σ_{t - j}^{2} \end{aligned}$ where $u_{t} \sim N (0, 1)$ .

GARCH(2,3) simulation

# Random seed 
set.seed(4)
# ==================== Setups =====================
# Number of simulations 
t_bar <- 500 
# Parameters
par <- c(mu=0.5, omega=0.4, 
         alpha1=0.05, alpha1=0.03, 
         beta1=0.55, beta2=0.15, beta3=0.05) 
# Long-term std deviation of residuals 
sigma_eps <- sqrt(par[2]/(1 - sum(par[3:7])))
# ================== Simulation ===================
# Initial points
Xt <- rep(par[1], 4)
sigma <- rep(sigma_eps, 4)
# Simulated residuals 
eps <- rnorm(t_bar, 0, 1) 
for(t in 4:t_bar){
  # ARCH(2) variance 
  sigma2_arch <- par[3]*eps[t-1]^2 + par[4]*eps[t-2]^2
  # GARCH(3) variance 
  sigma2_garch <- par[5]*sigma[t-1]^2 + par[6]*sigma[t-2]^2 + par[7]*sigma[t-3]^2
  # GARCH(2,3) std. deviation 
  sigma[t] <- sqrt(par[2] + sigma2_arch + sigma2_garch)
  # Simulated residuals 
  eps[t] <- sigma[t]*eps[t]
  # Simulated time series 
  Xt[t] <- par[1] + eps[t]
}
# ===================== Plot ======================
# GARCH(2,3) simulation
plot_garch <- ggplot()+
  geom_line(aes(1:t_bar, Xt), size = 0.2)+
  geom_line(aes(1:t_bar, par[1]), color = "red")+
  theme_bw()+
  labs(x = NULL, y = TeX("$X_t$"),
       subtitle = TeX(paste0("$\\mu:\\;", par[1], 
                             "\\;\\; \\omega:\\;", par[2], 
                             "\\;\\; \\alpha_{1}:\\;", par[3],
                             "\\;\\; \\alpha_{2}:\\;", par[4],
                             "\\;\\; \\beta_{1}:\\;", par[5],
                             "\\;\\; \\beta_{2}:\\;", par[6],
                             "\\;\\; \\beta_{3}:\\;", par[7],
                             "\\;\\; E\\{\\sigma_t\\}:\\;", sigma_eps,
                             "$")))
# GARCH(2,3) std. deviation
plot_sigma <- ggplot()+
  geom_line(aes(1:t_bar, sigma), alpha = 1)+
  geom_line(aes(1:t_bar, sigma_eps), color = "blue")+
  labs(x = "t", y = TeX("$\\sigma_{t}$"))+
  theme_bw()
gridExtra::grid.arrange(plot_garch, plot_sigma, heights = c(0.6, 0.4))

2.3 Example: GARCH(3,2) process

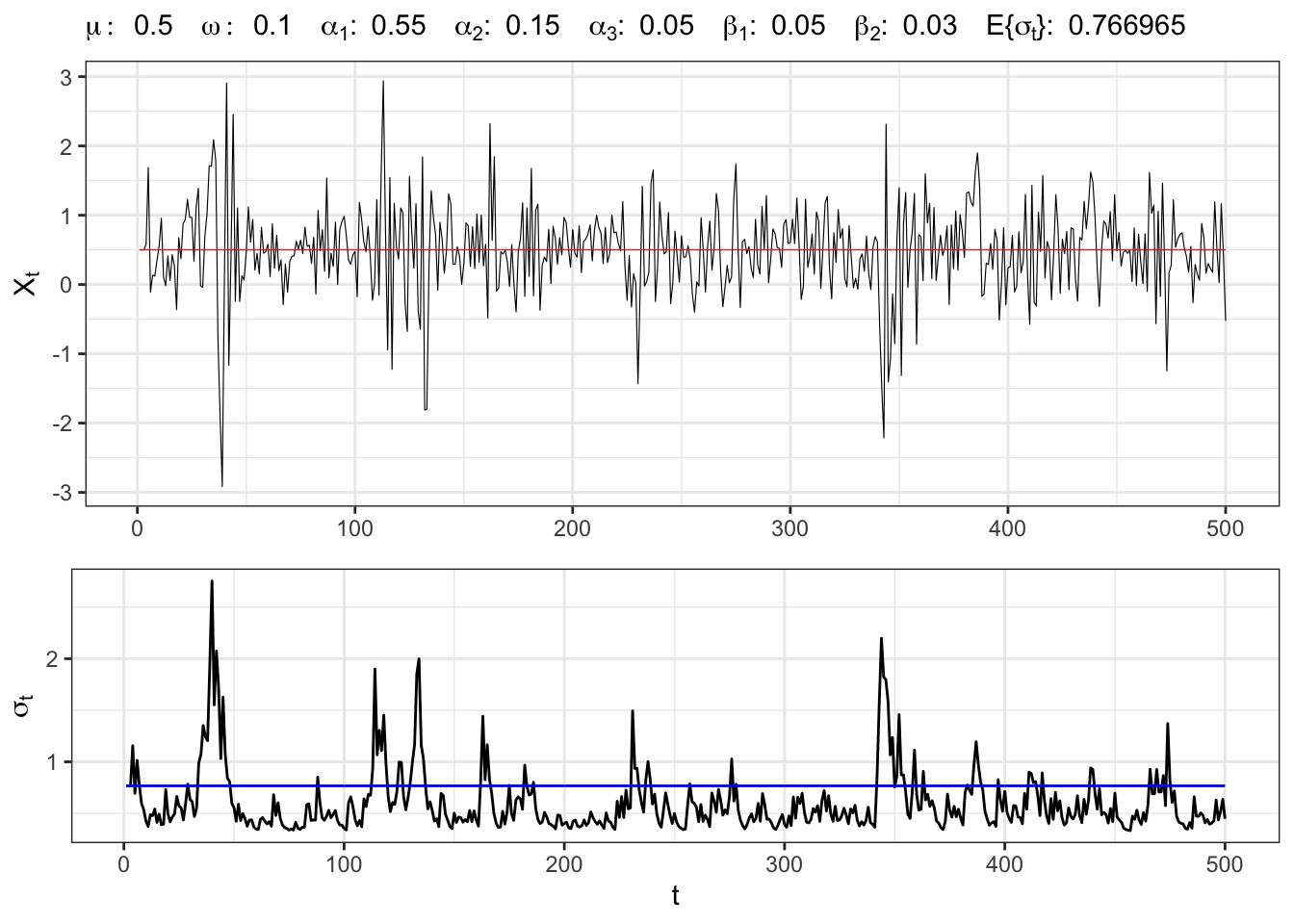
Let’s simulate an GARCH(3,2) process with normal residuals, namely $X_{t} \sim G A R C H (3, 2)$ , i.e. $\begin{aligned} x_{t} = μ + e_{t} \\ e_{t} = σ_{t} u_{t} \\ σ_{t}^{2} = ω + \sum_{i = 1}^{3} α_{i} e_{t - i}^{2} + \sum_{j = 1}^{2} β_{j} σ_{t - j}^{2} \end{aligned}$ where $u_{t} \sim N (0, 1)$ .

GARCH(3,2) simulation

# Random seed 
set.seed(5)
# ==================== Setups =====================
# Number of simulations 
t_bar <- 500 
# Parameters
par <- c(mu = 0.5, omega = 0.1, alpha1 = 0.55, 
         alpha2 = 0.15, alpha3 = 0.05, 
         beta1 = 0.05, beta2 = 0.03) 
# Long-term std deviation of residuals 
sigma_eps <- sqrt(par[2]/(1 - sum(par[3:7])))
# ================== Simulation ===================
# Initial points
Xt <- rep(par[1], 4)
sigma <- rep(sigma_eps, 4)
# Simulated residuals 
eps <- rnorm(t_bar, 0, 1) 
for(t in 4:t_bar){
  # ARCH(3) variance 
  sigma2_arch <- par[3]*eps[t-1]^2 + par[4]*eps[t-2]^2 + par[5]*eps[t-3]^2
  # GARCH(2) variance 
  sigma2_garch <- par[6]*sigma[t-3]^2 + par[7]*sigma[t-2]^2
  # GARCH(3,2) std. deviation 
  sigma[t] <- sqrt(par[2] + sigma2_arch + sigma2_garch)
  # Simulated residuals 
  eps[t] <- sigma[t]*eps[t]
  # Simulated time series 
  Xt[t] <- par[1] + eps[t]
}
# ===================== Plot ======================
# GARCH(3,2) simulation
plot_garch <- ggplot()+
  geom_line(aes(1:t_bar, Xt), size = 0.2)+
  geom_line(aes(1:t_bar, par[1]), color = "red", size = 0.2)+
  theme_bw()+
  labs(x = NULL, y = TeX("$X_t$"),
       subtitle = TeX(paste0("$\\mu:\\;", par[1], 
                             "\\;\\; \\omega:\\;", par[2], 
                             "\\;\\; \\alpha_{1}:\\;", par[3],
                             "\\;\\; \\alpha_{2}:\\;", par[4],
                             "\\;\\; \\alpha_{3}:\\;", par[5],
                             "\\;\\; \\beta_{1}:\\;", par[6],
                             "\\;\\; \\beta_{2}:\\;", par[7],
                             "\\;\\; E\\{\\sigma_t\\}:\\;", sigma_eps,
                             "$")))
# GARCH(3,2) std. deviation
plot_sigma <- ggplot()+
  geom_line(aes(1:t_bar, sigma), alpha = 1)+
  geom_line(aes(1:t_bar, sigma_eps), color = "blue")+
  labs(x = "t", y = TeX("$\\sigma_{t}$"))+
  theme_bw()
gridExtra::grid.arrange(plot_garch, plot_sigma, heights = c(0.6, 0.4))

3 IGARCH

Integrated Generalized Autoregressive Conditional heteroskedasticity (IGARCH(p,q)) is a restricted version of the GARCH model, where the persistent parameters sum up to one, and imports a unit root in the GARCH process. The condition for this is

$\sum_{i = 1}^{p} α_{i} + \sum_{j = 1}^{q} β_{j} = 1$

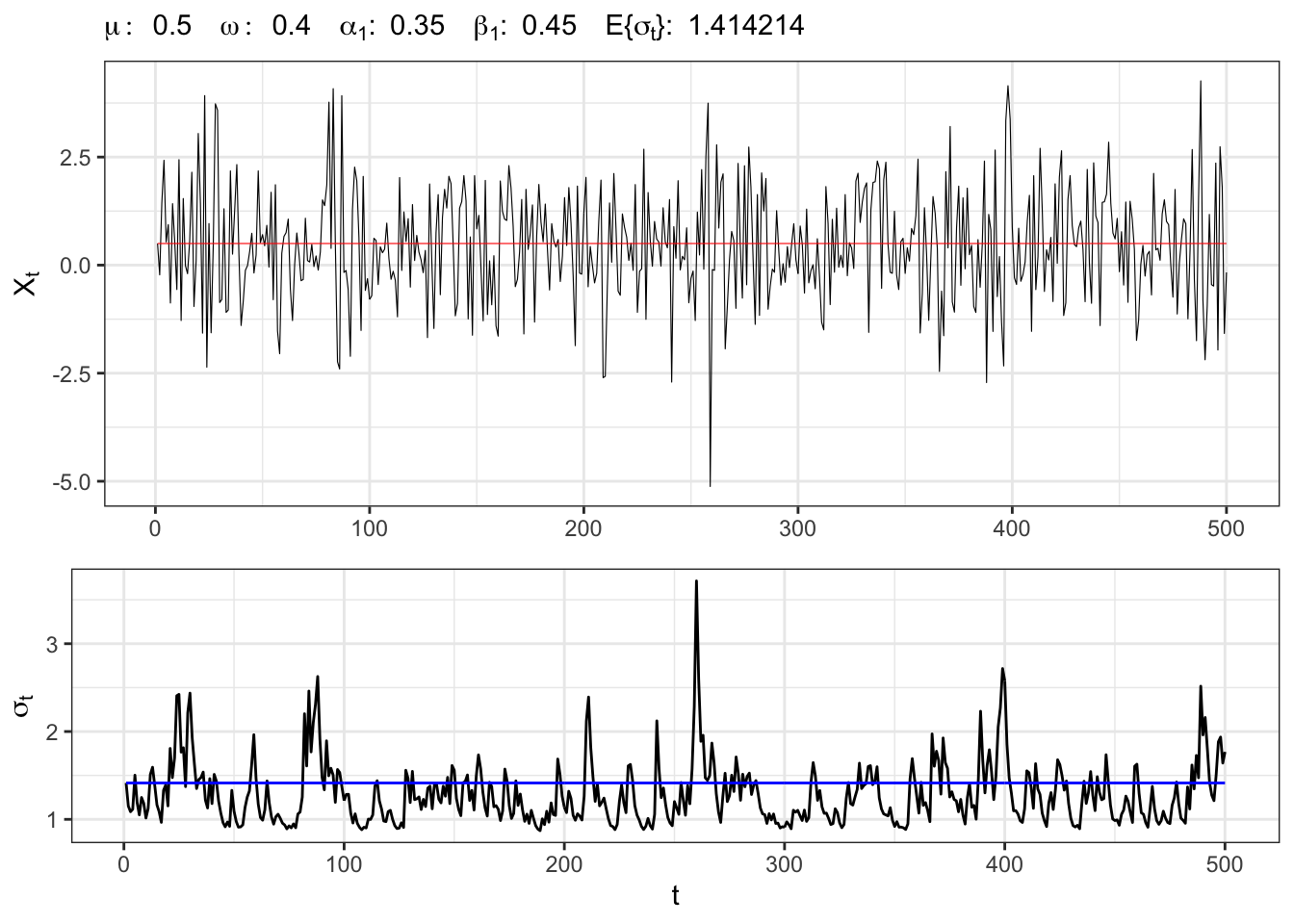
3.1 Example: IGARCH(1,1)

IGARCH(1,1) simulation

# Random seed 
set.seed(6)
# ==================== Setups =====================
# number of simulations 
t_bar <- 500 
# parameters
par <- c(mu=0.5, omega=0.4, alpha1=0.35, beta1=0.45) 
# long-term std deviation of residuals 
sigma_eps <- sqrt(par[2]/(1 - par[3] - par[4]))
# ================== Simulation ===================
# Initial points
Xt <- rep(par[1], 1)
sigma <- rep(sigma_eps, 1)
# Simulated residuals 
eps <- rnorm(t_bar, 0, 1) 
for(t in 2:t_bar){
  # iGARCH(1,1) variance 
  sigma[t] <- par[3]*eps[t-1]^2 + par[4]*sigma[t-1]^2
  # iGARCH std. deviation 
  sigma[t] <- sqrt(par[2] + sigma[t])
  # Simulated residuals 
  eps[t] <- sigma[t]*eps[t]
  # Simulated time series 
  Xt[t] <- par[1] + eps[t]
}
# ===================== Plot ======================
# iGARCH(1,1) simulation
plot_garch <- ggplot()+
  geom_line(aes(1:t_bar, Xt), size = 0.2)+
  geom_line(aes(1:t_bar, par[1]), color = "red", size = 0.2)+
  theme_bw()+
  labs(x = NULL, y = TeX("$X_t$"),
       subtitle = TeX(paste0("$\\mu:\\;", par[1], 
                             "\\;\\; \\omega:\\;", par[2], 
                             "\\;\\; \\alpha_{1}:\\;", par[3],
                             "\\;\\; \\beta_{1}:\\;", par[4],
                             "\\;\\; E\\{\\sigma_t\\}:\\;", sigma_eps,
                             "$")))
# iGARCH(1,1) std. deviation
plot_sigma <- ggplot()+
  geom_line(aes(1:t_bar, sigma), alpha = 1)+
  geom_line(aes(1:t_bar, sigma_eps), alpha = 1, color = "blue")+
  labs(x = "t", y = TeX("$\\sigma_{t}$"))+
  theme_bw()
gridExtra::grid.arrange(plot_garch, plot_sigma, heights = c(0.6, 0.4))

4 GARCH-M

The GARCH in-mean (GARCH-M) model adds a stochastic term into the mean equation, i.e.

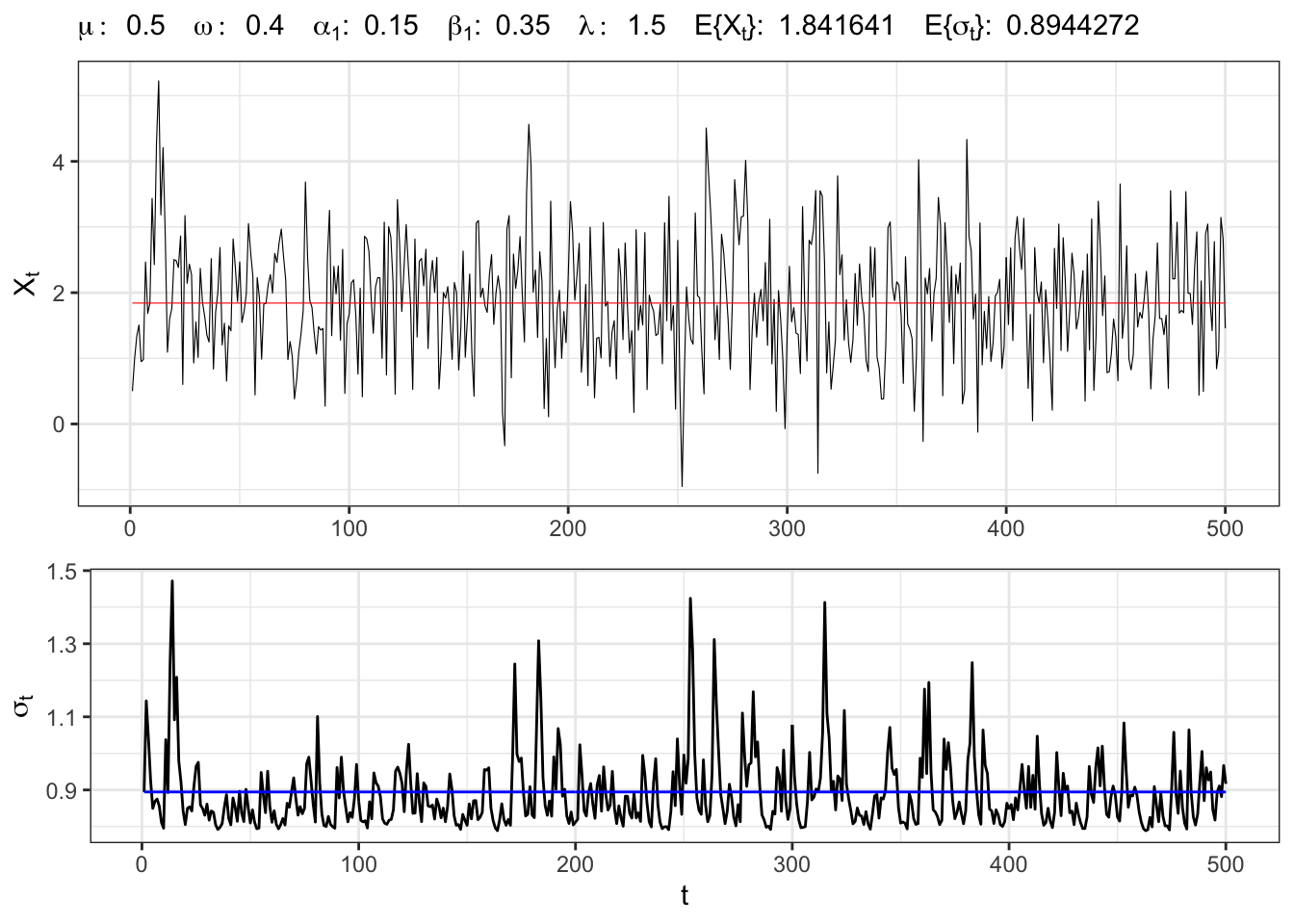
$\begin{aligned} x_{t} = μ + σ_{t} λ + e_{t} \\ e_{t} = σ_{t} u_{t} \\ σ_{t}^{2} = ω + \sum_{i = 1}^{p} α_{i} e_{t - i}^{2} + \sum_{j = 1}^{q} β_{j} σ_{t - j}^{2} \end{aligned}$ The effect of the parameter $λ$ is a shift of the mean of the process. The unconditional mean became $E {X_{t}} = μ + E {σ_{t}} λ$

4.1 Example: GARCH-M(1,1)

GARCH-M(1,1) simulation


set.seed(7)
# ==================== Setups =====================
# number of simulations 
t_bar <- 500 
# parameters
par <- c(mu=0.5, omega=0.4, 
         alpha1=0.15, beta1=0.35, lambda = 1.5) 
# long-term std deviation of residuals 
sigma_eps <- sqrt(par[2]/(1 - par[3] - par[4]))
# ================== Simulation ===================
# Initial points
Xt <- rep(par[1], 1)
sigma <- rep(sigma_eps, 1)
# Simulated residuals 
eps <- rnorm(t_bar, 0, 1) 
eps[1:2] <- eps[1:2]*sigma_eps
for(t in 2:t_bar){
  # GARCH(1,1) variance 
  sigma[t] <- par[3]*eps[t-1]^2 + par[4]*sigma[t-1]^2
  # GARCH std. deviation 
  sigma[t] <- sqrt(par[2] + sigma[t])
  # Simulated residuals 
  eps[t] <- sigma[t]*eps[t] 
  # Simulated time series 
  Xt[t] <- par[1] + sigma[t]*par[5] + eps[t]
}
# ===================== Plot ======================
# GARCH-M(1,1) simulation
plot_garch <- ggplot()+
  geom_line(aes(1:t_bar, Xt), size = 0.2)+
  geom_line(aes(1:t_bar, par[1] + sigma_eps*par[5]), color = "red", size = 0.2)+
  theme_bw()+
  labs(x = NULL, y = TeX("$X_t$"),
       subtitle = TeX(paste0("$\\mu:\\;", par[1], 
                             "\\;\\; \\omega:\\;", par[2], 
                             "\\;\\; \\alpha_{1}:\\;", par[3],
                             "\\;\\; \\beta_{1}:\\;", par[4],
                             "\\;\\; \\lambda:\\;", par[5],
                             "\\;\\; E\\{\\X_t\\}:\\;", par[1] + sigma_eps*par[5],
                             "\\;\\; E\\{\\sigma_t\\}:\\;", sigma_eps,
                             "$")))
# GARCH-M(1,1) std. deviation
plot_sigma <- ggplot()+
  geom_line(aes(1:t_bar, sigma), alpha = 1)+
  geom_line(aes(1:t_bar, sigma_eps), alpha = 1, color = "blue")+
  labs(x = "t", y = TeX("$\\sigma_{t}$"))+
  theme_bw()
gridExtra::grid.arrange(plot_garch, plot_sigma, heights = c(0.6, 0.4))

Citation

BibTeX citation:

@online{sartini2024,
  author = {Sartini, Beniamino},
  title = {ARCH-GARCH Process},
  date = {2024-05-01},
  url = {https://greenfin.it/statistics/arch-garch-process.html},
  langid = {en}
}

For attribution, please cite this work as:

Sartini, Beniamino. 2024. “ARCH-GARCH Process.” May 1, 2024. https://greenfin.it/statistics/arch-garch-process.html.