Gaussian mixture
Let’s consider a linear combination of a Bernoulli and two normal random variables, all assumed to be independent, i.e.
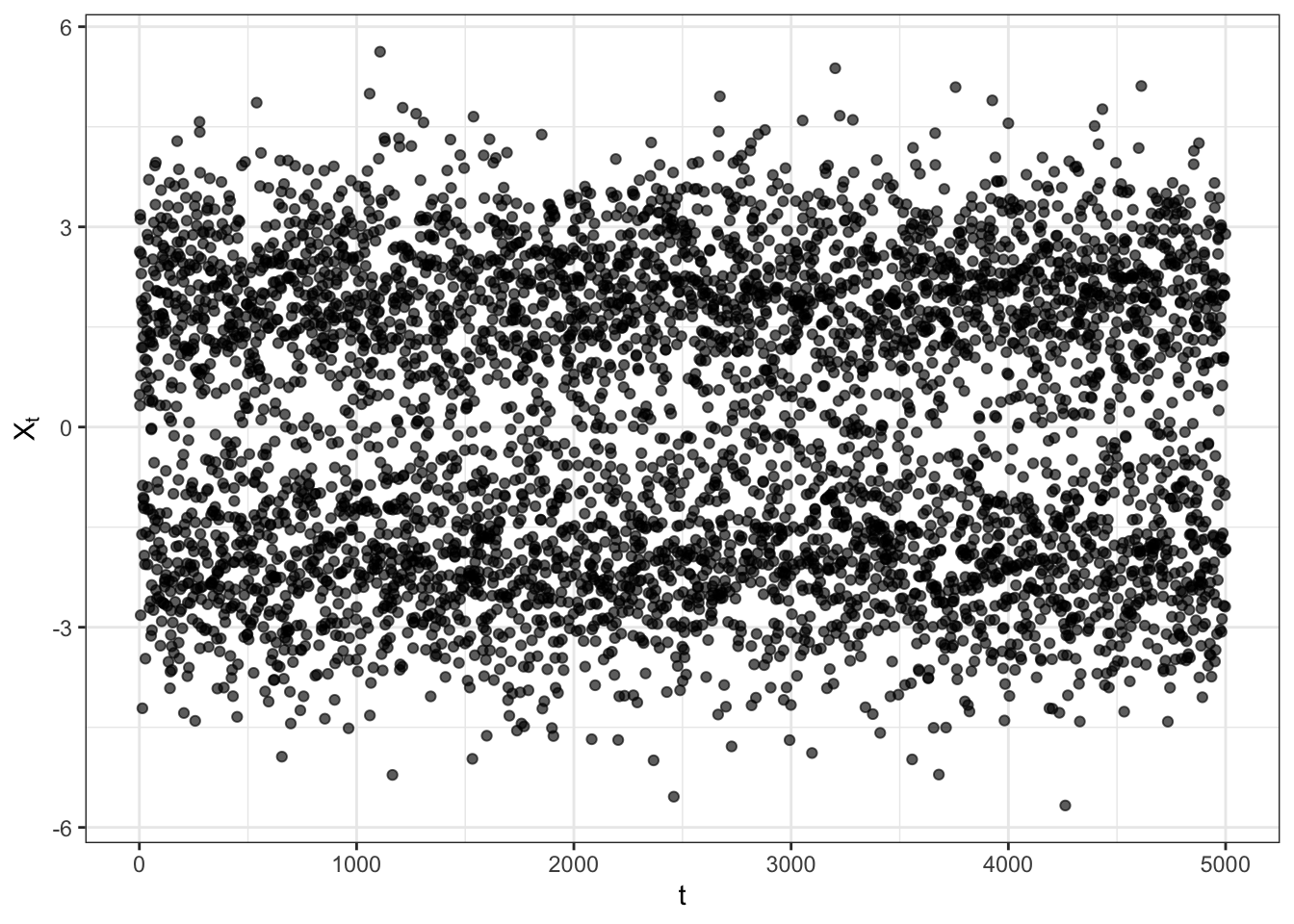
Gaussian mixture simulation
# ================== Setups ==================
t_bar <- 5000 # number of steps ahead
# parameters
par <- c(mu1=-2,mu2=2,sd1=1,sd2=1,p=0.5)
# ============================================
# Gaussian mixture simulation
N_1 <- rnorm(t_bar, mean = par[1], sd = par[3])
N_2 <- rnorm(t_bar, mean = par[2], sd = par[4])
B <- rbinom(t_bar, 1, prob = par[5])
Xt <- B*N_1 + (1 - B)*N_2
# Empiric pdf and cdf
ker <- density(Xt, from = min(Xt), to = max(Xt))
ker$cdf_emp <- cumsum(ker$y/sum(ker$y))
# Components normal pdf
ker$pdf_Z1 <- dnorm(ker$x, mean = par[1], sd = par[3])
ker$pdf_Z2 <- dnorm(ker$x, mean = par[2], sd = par[4])
# Mixture pdf and cdf
ker$pdf <- par[5]*ker$pdf_Z1 + (1-par[5])*ker$pdf_Z2
ker$cdf <- cumsum(ker$pdf/sum(ker$pdf))
# =================== Plot ===================
# Plot trajectory
plot_gm <- ggplot()+
geom_point(aes(1:t_bar, Xt), alpha = exp(-0.00009*t_bar))+
labs(x = "t", y = TeX("$X_t$"))+
theme_bw()
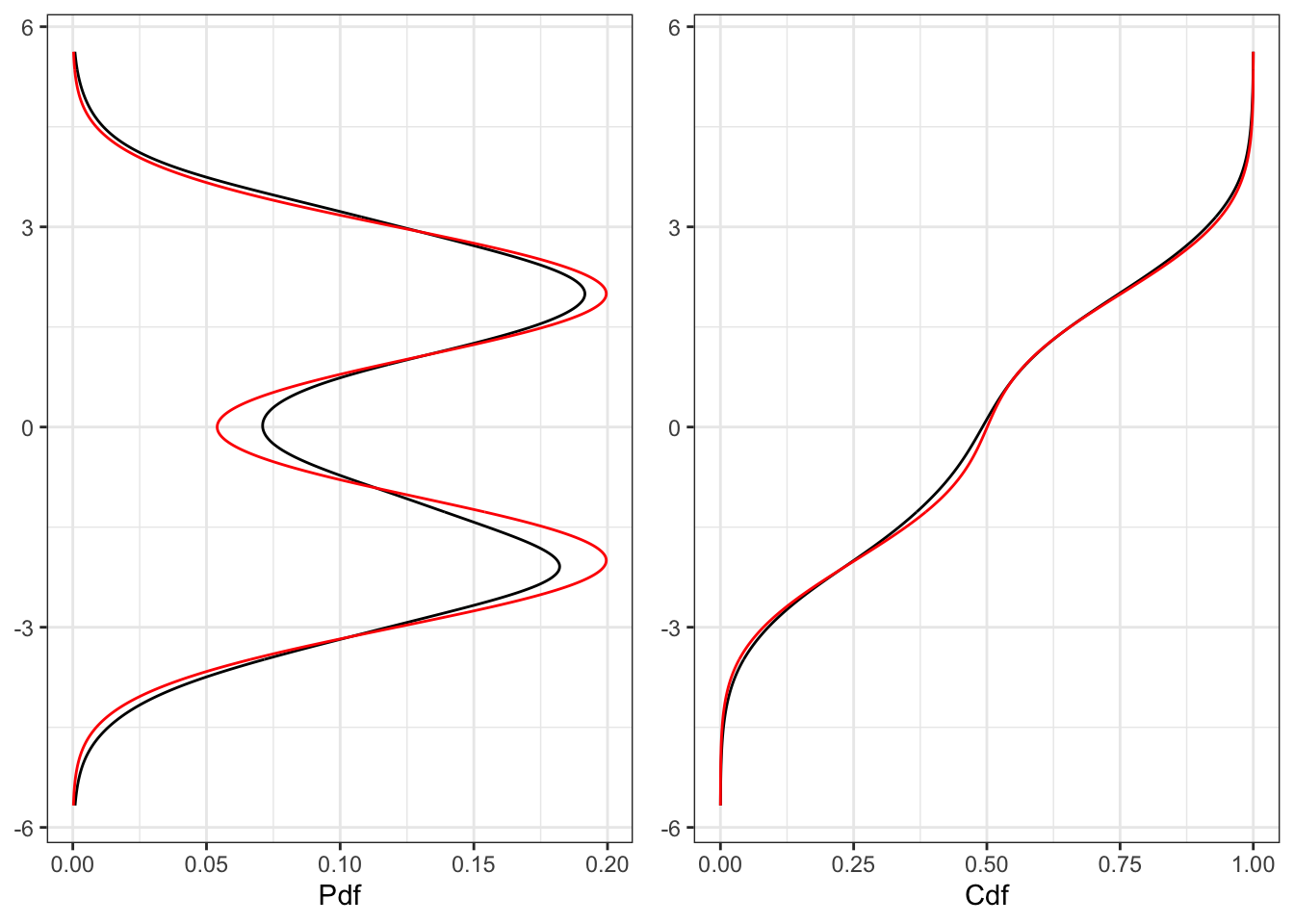
# Plot pdf
plot_pdf <- ggplot()+
geom_line(aes(ker$x, ker$y))+
geom_line(aes(ker$x, ker$pdf), color = "red")+
labs(x = NULL, y = "Pdf")+
theme_bw()+
coord_flip()
# Plot cdf
plot_cdf <- ggplot()+
geom_line(aes(ker$x, ker$cdf_emp))+
geom_line(aes(ker$x, ker$cdf), color = "red")+
labs(x = NULL, y = "Cdf")+
theme_bw()+
coord_flip()
plot_gm
gridExtra::grid.arrange(plot_pdf, plot_cdf, ncol = 2)1 Distribution and density
The distribution function of a Gaussian mixture reads explicitely as:
dnorm_mix <- function(params) {
# parameters
mu1 = params[1]
mu2 = params[2]
sd1 = params[3]
sd2 = params[4]
p = params[5]
function(x, log = FALSE){
probs <- p*stats::dnorm(x, mean = mu1, sd = sd1) + (1-p)*stats::dnorm(x, mean = mu2, sd = sd2)
if (log) {
probs <- base::log(probs)
}
return(probs)
}
}Proof. The distribution function of a Gaussian Mixture is defined as:
2 Moments
Given that
Proof. Given that
3 Maximum likelihood
Minimizing the negative log-likelihood gives an estimate of the parameters, i.e.
Maximum likelihood for Gaussian mixture
# Initialize parameters
init_params <- par*runif(5, 0.3, 1.1)
# Log-likelihood function
log_lik <- function(params, x){
# Parameters
mu1 = params[1]
mu2 = params[2]
sd1 = params[3]
sd2 = params[4]
p = params[5]
# Ensure that probability is in (0,1)
if(p > 0.99 | p < 0.01 | sd1 < 0 | sd2 < 0){ s
return(NA_integer_)
}
# Mixture density
pdf_mix <- dnorm_mix(params)
# Log-likelihood
loss <- sum(pdf_mix(x, log = TRUE), na.rm = TRUE)
return(loss)
}
# Optimal parameters
# fnscale = -1 to maximize (or use negative likelihood)
ml_estimate <- optim(par = init_params, log_lik,
x = Xt, control = list(maxit = 500000, fnscale = -1))4 Moments matching
Let’s fix the parameter of the first component, namely
5 Moment generating function
The moment generating function of a Gaussian mixture random variable (Equation 1) reads:
Proof. Applying the definition of moment generating function on a gaussian mixture we obtain:
6 Esscher transform
The Esscher transform of a Gaussian mixture random variable reads:
Proof. In general, the Esscher transform of a density function is computed as:
Citation
@online{sartini2024,
author = {Sartini, Beniamino},
title = {Gaussian Mixture},
date = {2024-05-01},
url = {https://greenfin.it/statistics/distributions/gaussian-mixture.html},
langid = {en}
}