Tukey functions

Author

Affiliation

Beniamino Sartini

University of Bologna

Published

May 1, 2024

Modified

June 16, 2024

Setup

library(dplyr)
# required for figures  
library(ggplot2)
# required for render latex 
library(backports)
library(latex2exp)
# Random seed 
set.seed(1)
# Grid of points
grid <- seq(-6, 6, 0.01)
# Grid of "d" parameter
d <- c(4.57, 3.57, 2.57, 1.57)

1 Tukey’s Bisquare

$ρ_{d} (x) = {\begin{cases} \begin{aligned} \frac{d^{2}}{6} {1 - {[1 - \frac{x^{2}}{d^{2}}]}^{3}} & | x | \leq d \\ \frac{d^{2}}{6} & | x | > d \end{aligned} \end{cases}$

tukey_bisquare <- function(d){
  function(x){
    x[abs(x) > d] <- NA
    f_x <- (d^2)/6*(1 - (1 - (x/d)^2)^3)
    f_x[is.na(f_x)] <- (d^2)/6
    return(f_x)
  }
}

Plot code

ggplot()+
  geom_line(aes(grid, tukey_bisquare(d[1])(grid), color = "p1"))+
  geom_line(aes(grid, tukey_bisquare(d[2])(grid), color = "p2"))+
  geom_line(aes(grid, tukey_bisquare(d[3])(grid), color = "p3"))+
  geom_line(aes(grid, tukey_bisquare(d[4])(grid), color = "p4"))+
  scale_color_manual(values = c(p1 = "red", p2 = "black", p3 = "green", p4 = "purple"),
                     labels = c(p1 = paste0("d = ", d[1]), 
                                p2 = paste0("d = ", d[2]), 
                                p3 = paste0("d = ", d[3]), 
                                p4 = paste0("d = ", d[4])))+
  theme_bw()+
  scale_x_continuous(breaks = c(min(grid),-d, 0, d, max(grid)))+
  theme(legend.position = "top")+
  labs(x = "x", y = TeX("$\\rho(x; d)$"), color = NULL)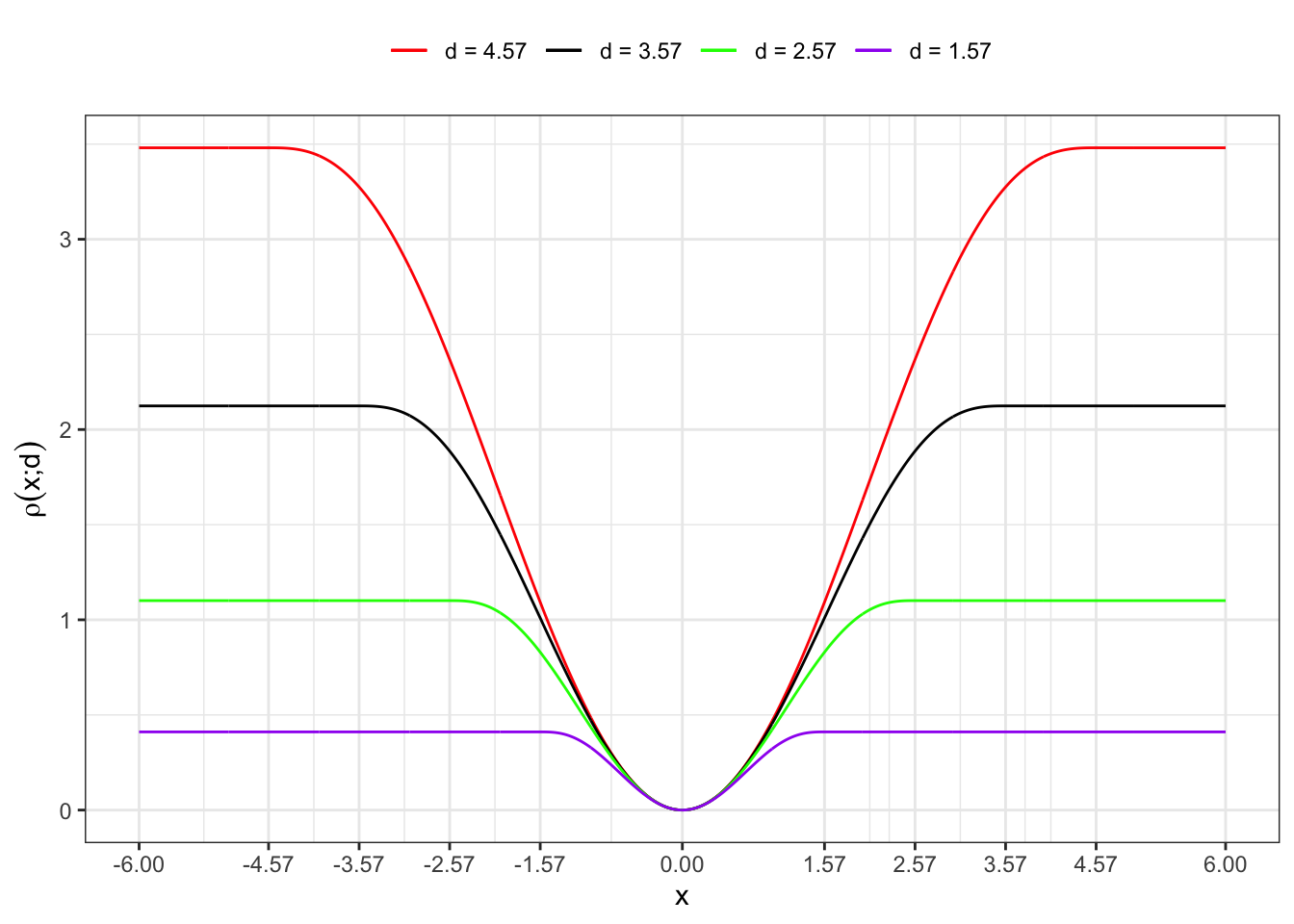

1.1 First derivative

$ρ^{'} (x; d) = {\begin{cases} \begin{aligned} x {[1 - \frac{x^{2}}{d^{2}}]}^{2} & | x | \leq d \\ 0 & | x | > d \end{aligned} \end{cases}$

# Tukey's Bisquare First Derivative
tukey_bisquare_prime <- function(d){
  function(x){
    x[abs(x) > d] <- NA
    f_x <- x*(1 - (x/d)^2)^2
    f_x[is.na(f_x)] <- 0
    return(f_x)
  }
}

Plot code

ggplot()+
  geom_line(aes(grid, tukey_bisquare_prime(d[1])(grid), color = "p1"))+
  geom_line(aes(grid, tukey_bisquare_prime(d[2])(grid), color = "p2"))+
  geom_line(aes(grid, tukey_bisquare_prime(d[3])(grid), color = "p3"))+
  geom_line(aes(grid, tukey_bisquare_prime(d[4])(grid), color = "p4"))+
  scale_color_manual(values = c(p1 = "red", p2 = "black", p3 = "green", p4 = "purple"),
                     labels = c(p1 = paste0("d = ", d[1]), 
                                p2 = paste0("d = ", d[2]), 
                                p3 = paste0("d = ", d[3]), 
                                p4 = paste0("d = ", d[4])))+
  theme_bw()+
  scale_x_continuous(breaks = c(min(grid),-d, 0, d, max(grid)))+
  theme(legend.position = "top")+
  labs(x = "x", y = TeX("$\\rho^{\\prime}(x; d)$"), color = NULL)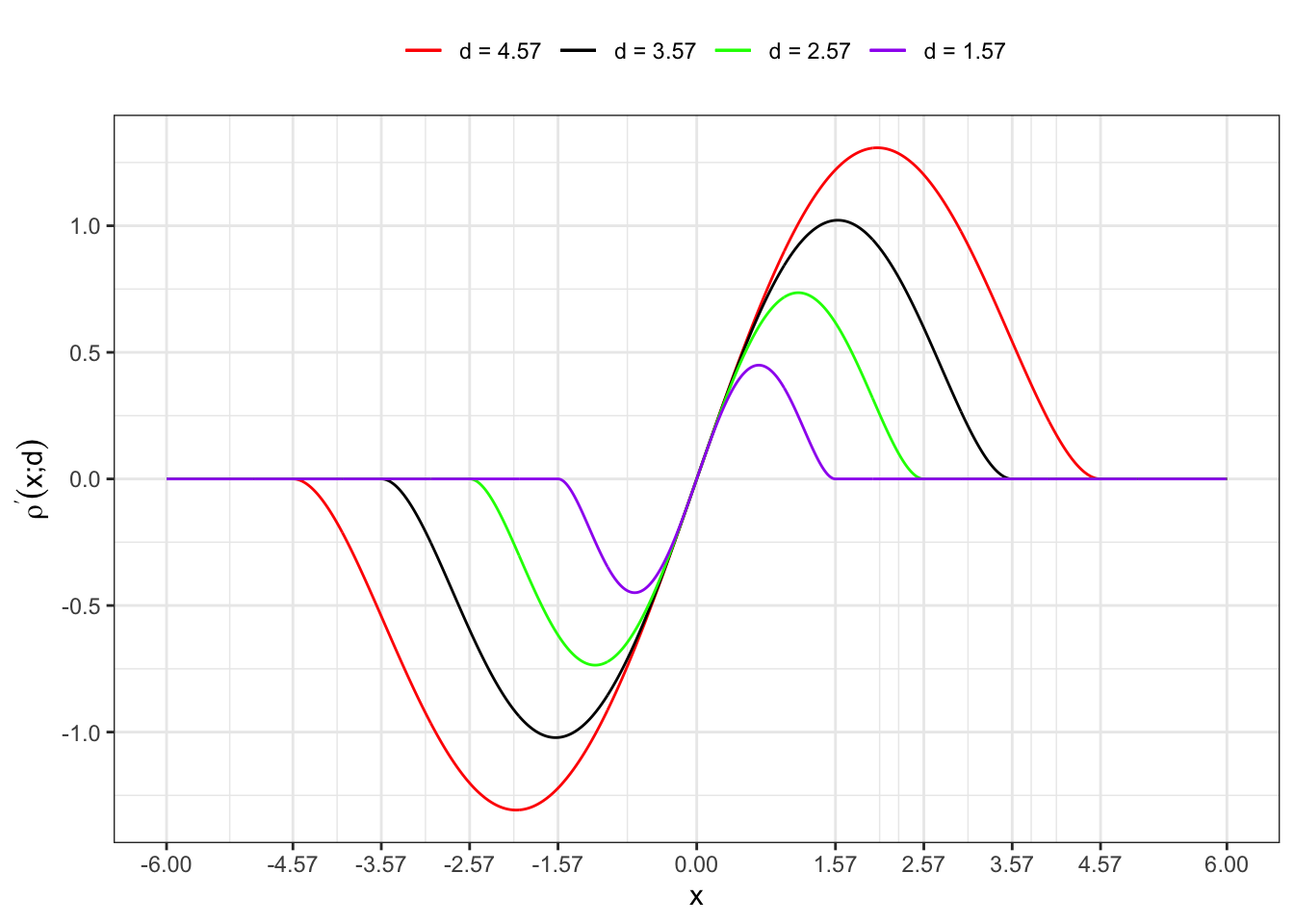

1.2 Second derivative

$ρ_{d}^{''} (x) = {\begin{cases} \begin{aligned} (1 - \frac{x^{2}}{d^{2}}) (1 - \frac{x^{2}}{d^{2}} - \frac{4 x^{2}}{d^{2}}) & | x | \leq d \\ 0 & | x | > d \end{aligned} \end{cases}$

# Tukey's Bisquare Second Derivative
tukey_bisquare_second <- function(d){
  function(x){
    x[abs(x) > d] <- NA
    f_x <- (1 - (x/d)^2)*((1 - (x/d)^2) - 4*(x^2)/(d^2))
    f_x[is.na(f_x)] <- 0
    return(f_x)
  }
}

Plot code

ggplot()+
  geom_line(aes(grid, tukey_bisquare_second(d[1])(grid), color = "p1"))+
  geom_line(aes(grid, tukey_bisquare_second(d[2])(grid), color = "p2"))+
  geom_line(aes(grid, tukey_bisquare_second(d[3])(grid), color = "p3"))+
  geom_line(aes(grid, tukey_bisquare_second(d[4])(grid), color = "p4"))+
  scale_color_manual(values = c(p1 = "red", p2 = "black", p3 = "green", p4 = "purple"),
                     labels = c(p1 = paste0("d = ", d[1]), 
                                p2 = paste0("d = ", d[2]), 
                                p3 = paste0("d = ", d[3]), 
                                p4 = paste0("d = ", d[4])))+
  theme_bw()+
  scale_x_continuous(breaks = c(min(grid),-d, 0, d, max(grid)))+
  theme(legend.position = "top")+
  labs(x = "x", y = TeX("$\\rho^{\\prime\\prime}(x; d)$"), color = NULL)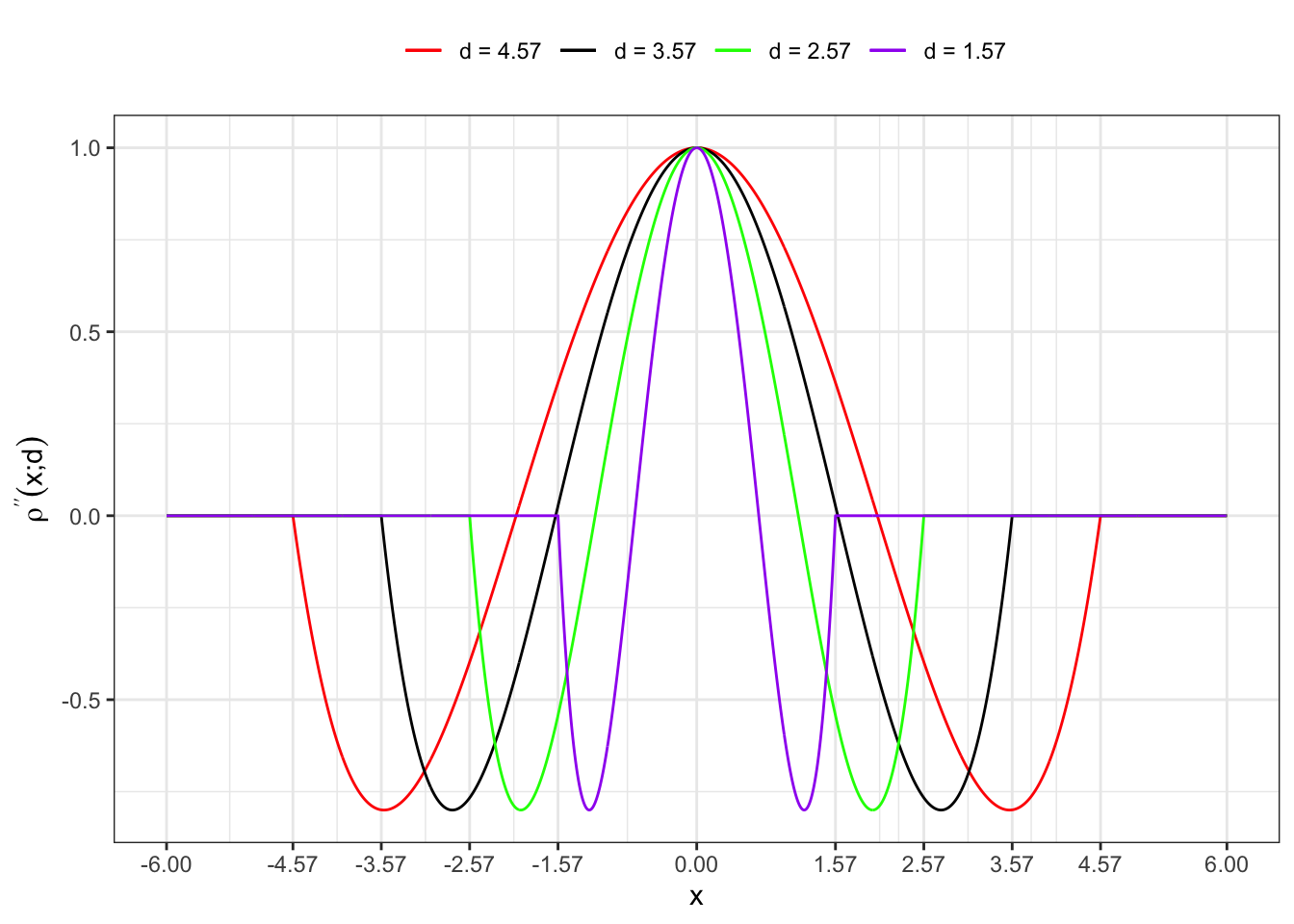

2 Tukey Biweight

$ρ_{d} (x) = {\begin{cases} \begin{aligned} {(1 - \frac{x^{2}}{d^{2}})}^{2} & | x | \leq d \\ 0 & | x | > d \end{aligned} \end{cases}$

# Tukey's Biweight Function
tukey_biweight <- function(d){
  function(x){
    x[abs(x) > d] <- NA
    f_x <- (1 - (x/d)^2)^2
    f_x[is.na(f_x)] <- 0
    return(f_x)
  }
}

Plot code

ggplot()+
  geom_line(aes(grid, tukey_biweight(d[1])(grid), color = "p1"))+
  geom_line(aes(grid, tukey_biweight(d[2])(grid), color = "p2"))+
  geom_line(aes(grid, tukey_biweight(d[3])(grid), color = "p3"))+
  geom_line(aes(grid, tukey_biweight(d[4])(grid), color = "p4"))+
  scale_color_manual(values = c(p1 = "red", p2 = "black", p3 = "green", p4 = "purple"),
                     labels = c(p1 = paste0("d = ", d[1]), 
                                p2 = paste0("d = ", d[2]), 
                                p3 = paste0("d = ", d[3]), 
                                p4 = paste0("d = ", d[4])))+
  theme_bw()+
  scale_x_continuous(breaks = c(min(grid),-d, 0, d, max(grid)))+
  theme(legend.position = "top")+
  labs(x = "x", y = TeX("$\\rho(x; d)$"), color = NULL)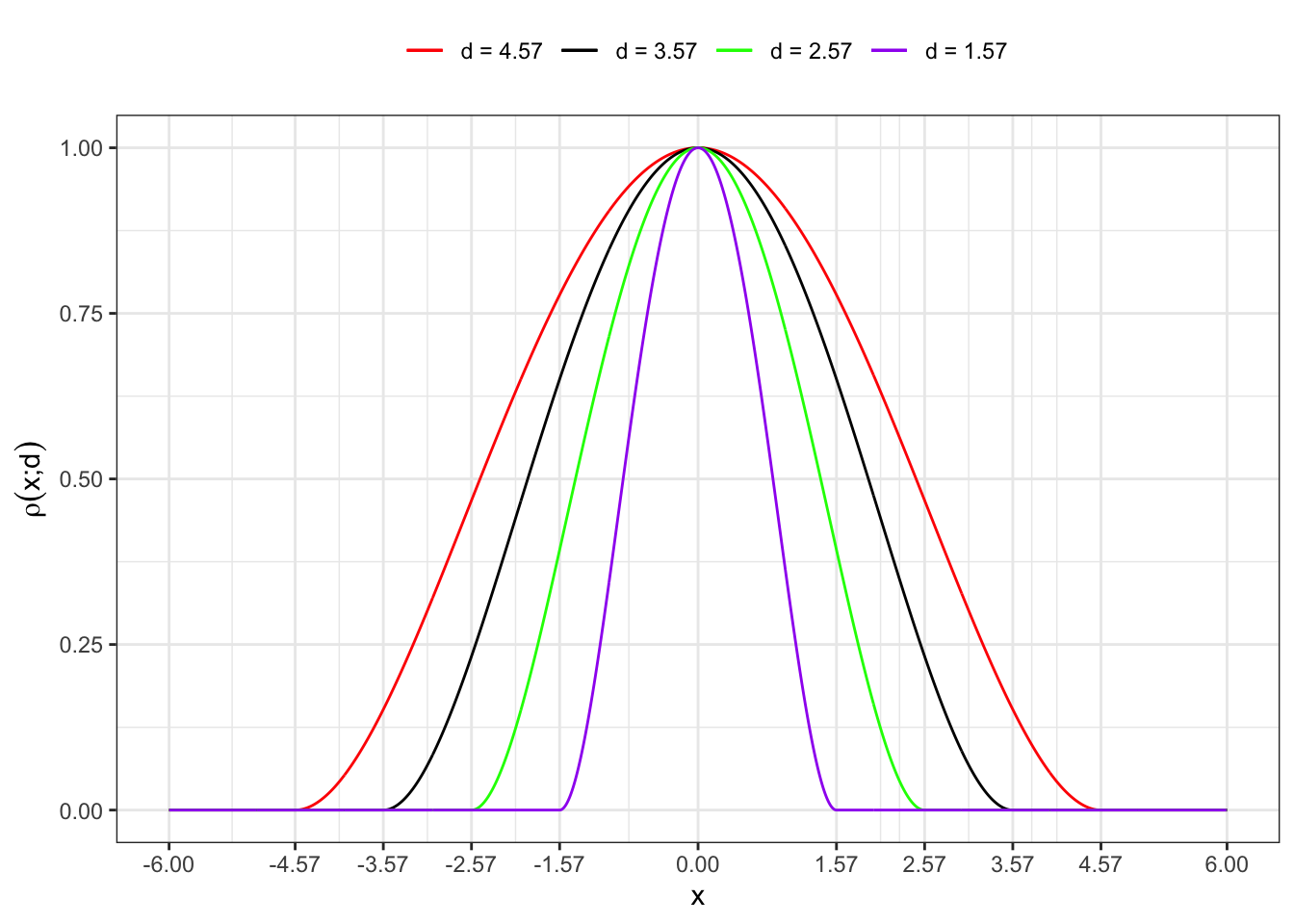

3 Tukey-Beaton Bisquare

$ρ_{d} (x) = {\begin{cases} \begin{aligned} \frac{3 x^{2}}{d^{2}} - \frac{3 x^{4}}{d^{4}} + \frac{x^{6}}{d^{6}} & | x | \leq d \\ 1 & | x | > d \end{aligned} \end{cases}$

# Tukey-Beaton Bisquare Function
tukey_beaton_bisquare <- function(d){
  function(x){
    x[abs(x) > d] <- NA
    f_x <- 3*(x/d)^2 - 3*(x/d)^4 + (x/d)^6
    f_x[is.na(f_x)] <- 1
    return(f_x)
  }
}

Plot code

ggplot()+
  geom_line(aes(grid, tukey_beaton_bisquare(d[1])(grid), color = "p1"))+
  geom_line(aes(grid, tukey_beaton_bisquare(d[2])(grid), color = "p2"))+
  geom_line(aes(grid, tukey_beaton_bisquare(d[3])(grid), color = "p3"))+
  geom_line(aes(grid, tukey_beaton_bisquare(d[4])(grid), color = "p4"))+
  scale_color_manual(values = c(p1 = "red", p2 = "black", p3 = "green", p4 = "purple"),
                     labels = c(p1 = paste0("d = ", d[1]), 
                                p2 = paste0("d = ", d[2]), 
                                p3 = paste0("d = ", d[3]), 
                                p4 = paste0("d = ", d[4])))+
  theme_bw()+
  scale_x_continuous(breaks = c(min(grid),-d, 0, d, max(grid)))+
  theme(legend.position = "top")+
  labs(x = "x", y = TeX("$\\rho(x; d)$"), color = NULL)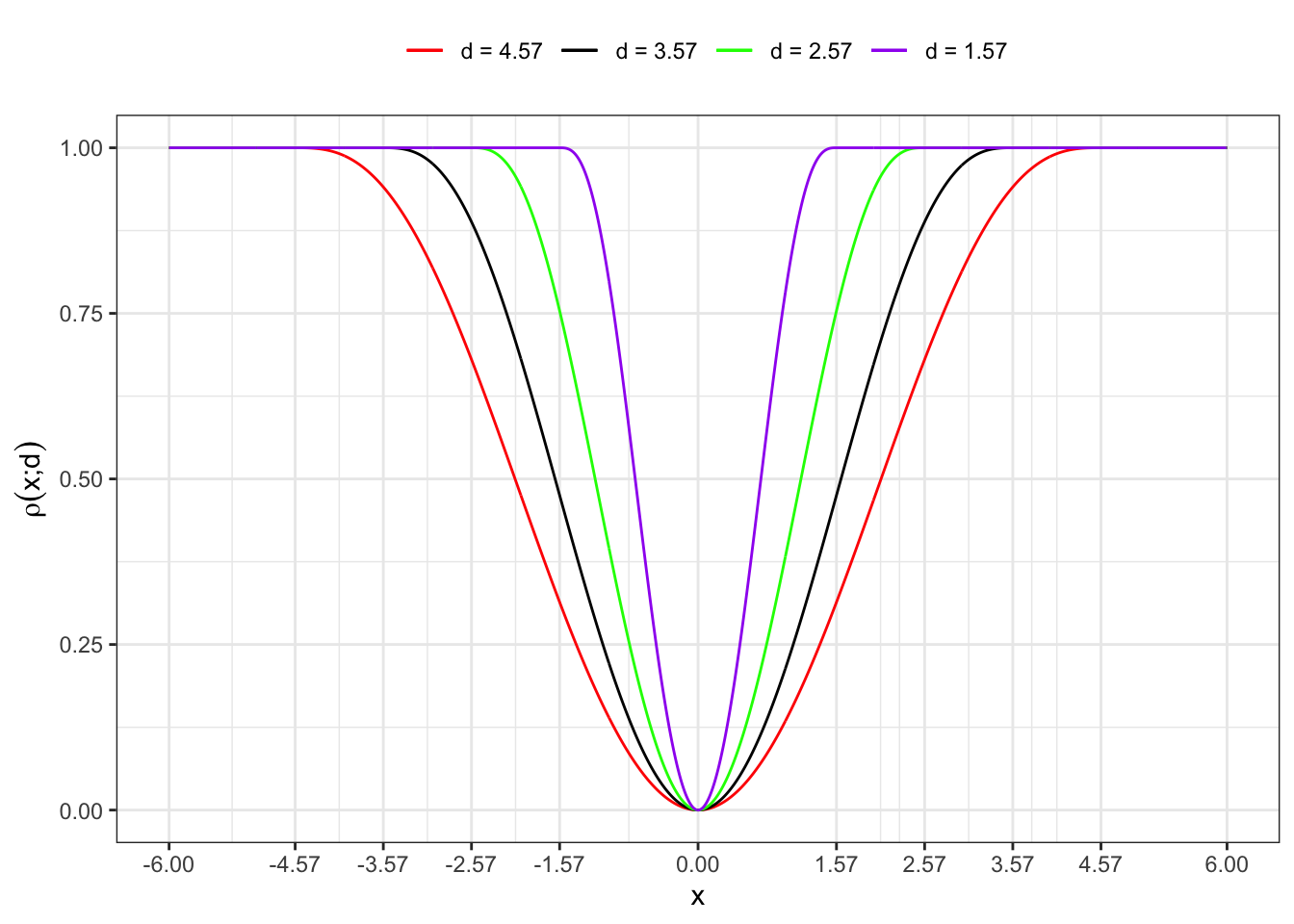

3.1 First derivative

$ρ_{d}^{'} (x) = {\begin{cases} \begin{aligned} \frac{6 x}{d^{2}} - \frac{12 x^{3}}{d^{4}} + \frac{6 x^{5}}{d^{4}} & | x | \leq d \\ 0 & | x | > d \end{aligned} \end{cases}$

# Tukey-Beaton Bisquare First Derivative
tukey_beaton_prime <- function(d){
  function(x){
    x[abs(x) > d] <- NA
    f_x <- 6*(1/d^2)*x - 12*(1/d^4)*(x)^3 + 6*(x)^5*(1/d^6)
    f_x[is.na(f_x)] <- 0
    return(f_x)
  }
}

Plot code

ggplot()+
  geom_line(aes(grid, tukey_beaton_prime(d[1])(grid), color = "p1"))+
  geom_line(aes(grid, tukey_beaton_prime(d[2])(grid), color = "p2"))+
  geom_line(aes(grid, tukey_beaton_prime(d[3])(grid), color = "p3"))+
  geom_line(aes(grid, tukey_beaton_prime(d[4])(grid), color = "p4"))+
  scale_color_manual(values = c(p1 = "red", p2 = "black", p3 = "green", p4 = "purple"),
                     labels = c(p1 = paste0("d = ", d[1]), 
                                p2 = paste0("d = ", d[2]), 
                                p3 = paste0("d = ", d[3]), 
                                p4 = paste0("d = ", d[4])))+
  theme_bw()+
  scale_x_continuous(breaks = c(min(grid),-d, 0, d, max(grid)))+
  theme(legend.position = "top")+
  labs(x = "x", y = TeX("$\\rho^{\\prime}(x; d)$"), color = NULL)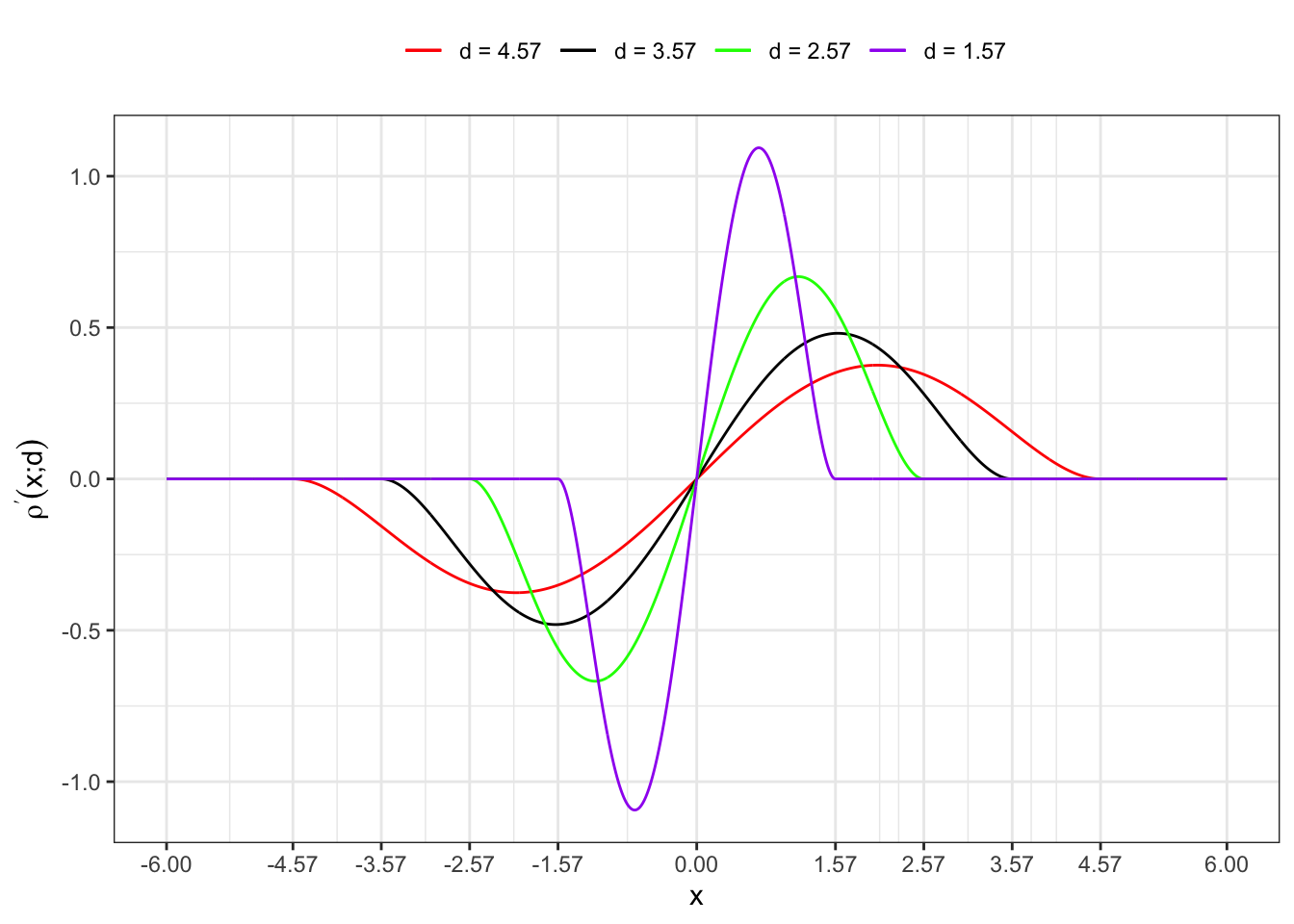

3.2 Second derivative

$ρ_{d}^{''} (x) = {\begin{cases} \begin{aligned} \frac{6}{d^{2}} - \frac{36 x^{2}}{d^{4}} + \frac{30 x^{4}}{d^{4}} & | x | \leq d \\ 0 & | x | > d \end{aligned} \end{cases}$

# Tukey-Beaton Bisquare Second Derivative
tukey_beaton_second <- function(d){
  function(x){
    x[abs(x) > d] <- NA
    f_x <- 6*(1/d^2) - 36*(1/d^4)*(x)^2 + 30*(x)^4*(1/d^6)
    f_x[is.na(f_x)] <- 0
    return(f_x)
  }
}

Plot code

ggplot()+
  geom_line(aes(grid, tukey_beaton_second(d[1])(grid), color = "p1"))+
  geom_line(aes(grid, tukey_beaton_second(d[2])(grid), color = "p2"))+
  geom_line(aes(grid, tukey_beaton_second(d[3])(grid), color = "p3"))+
  geom_line(aes(grid, tukey_beaton_second(d[4])(grid), color = "p4"))+
  scale_color_manual(values = c(p1 = "red", p2 = "black", p3 = "green", p4 = "purple"),
                     labels = c(p1 = paste0("d = ", d[1]), 
                                p2 = paste0("d = ", d[2]), 
                                p3 = paste0("d = ", d[3]), 
                                p4 = paste0("d = ", d[4])))+
  theme_bw()+
  scale_x_continuous(breaks = c(min(grid),-d, 0, d, max(grid)))+
  theme(legend.position = "top")+
  labs(x = "x", y = TeX("$\\rho^{\\prime\\prime}(x; d)$"), color = NULL)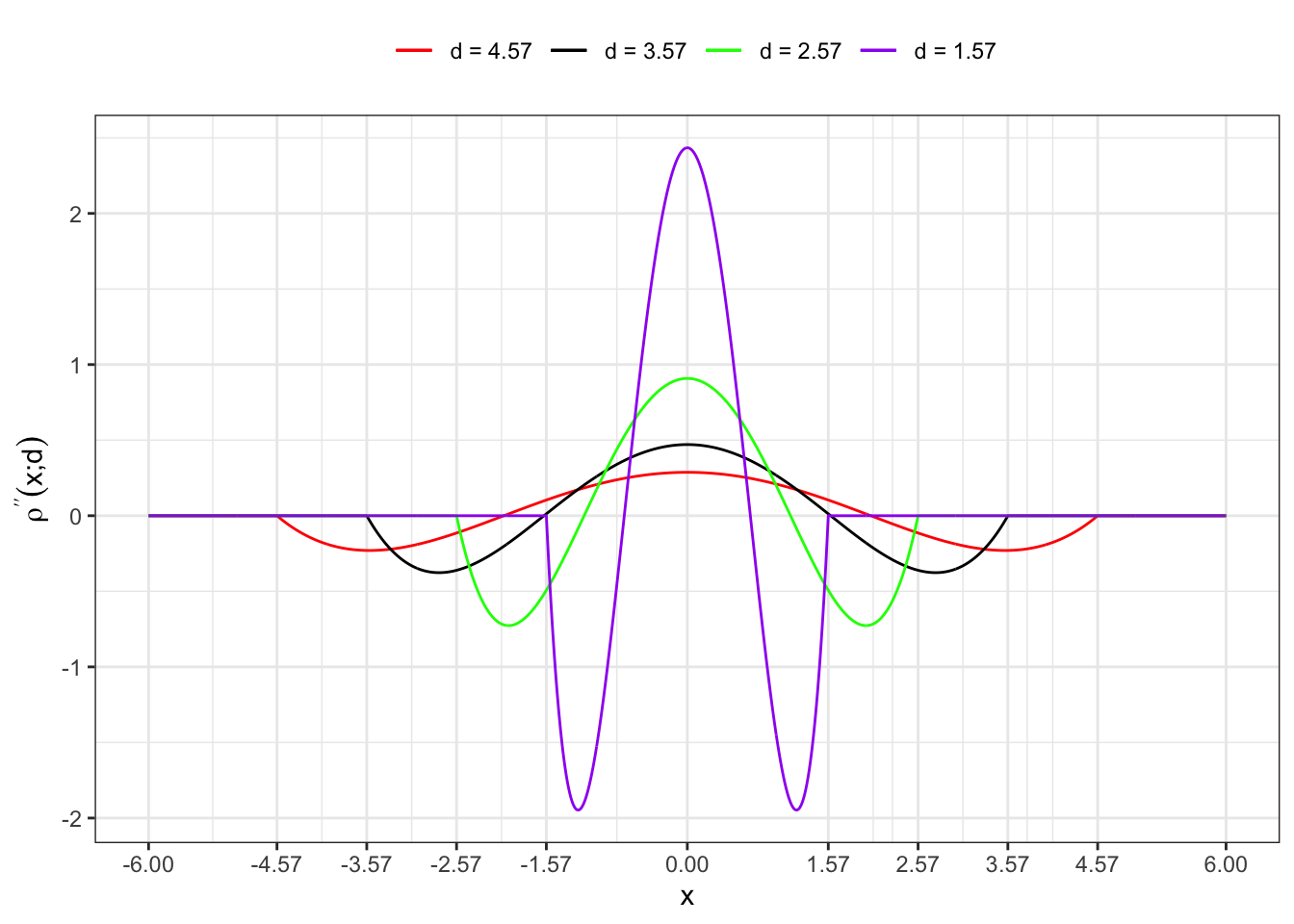

Citation

BibTeX citation:

@online{sartini2024,
  author = {Sartini, Beniamino},
  title = {Tukey Functions},
  date = {2024-05-01},
  url = {https://greenfin.it/statistics/robustness/tukey-functions.html},
  langid = {en}
}

For attribution, please cite this work as:

Sartini, Beniamino. 2024. “Tukey Functions.” May 1, 2024. https://greenfin.it/statistics/robustness/tukey-functions.html.