Author
Affiliation

Beniamino Sartini

University of Bologna

Published

June 21, 2025

Modified

June 21, 2025

1 Hourly energy demand generation and weather

Code 
library(tidyverse)
library(backports)
library(solarr)
library(latex2exp)

2 Description of the data

The dataset contains 4 years of electrical consumption, generation, pricing, and weather data for Spain. Consumption and generation data was retrieved from ENTSOE a public portal for Transmission Service Operator (TSO) data. Settlement prices were obtained from the Spanish TSO Red Electric España. Weather data was purchased as part of a personal project from the Open Weather API for the 5 largest cities in Spain. The original datasets can be downloaded from Kaggle. However, the dataset to be used for the project has been already pre-processed. The code used for preprocessing is in this github repository, while the dataset to be used can be downloaded here.

Tip 1: Variables description
  • date: datetime index localized to CET.
  • date_day: date without hour.
  • city: reference city. (Valencia. Madrid, Bilbao,Barcelona, Seville)
  • Year: number for the year.
  • Month: number for the month.
  • Day: number for the day in a month.
  • Hour: reference hour of the day.

Energy variables

  • fossil: energy produced with fossil sources: i.e. coal/lignite, natural gas, oil (MW).
  • nuclear: energy produced with nuclear sources (MW).
  • energy_other: other generation (MW).
  • solar: solar generation (MW).
  • biomass: biomass generation (MW).
  • river: hydroeletric generation (MW).
  • wind: wind generation (MW).
  • energy_other_renewable: other renewable generation (MW).
  • energy_waste: wasted generation (MW).
  • pred_solar: forecasted solar generation (MW).
  • pred_demand: forecasted electrical demand by TSO (MW).
  • pred_price: forecasted day ahead electrical price by TSO (Eur/MWh).
  • price: actual electrical price (Eur/MWh).
  • demand: actual electrical demand (Eur/MWh).
  • prod_tot: total electrical production (MW).
  • prod_renewable: total renewable electrical production (MW).

Weather variables

  • temp: mean temperature.
  • temp_min: minimum temperature (degrees).
  • temp_max: maximum temperature (degrees).
  • pressure: pressure in (hPas).
  • humidity: humidity in percentage.
  • wind_speed: wind speed (m/s).
  • wind_deg: wind direction.
  • rain_1h: rain in last hour (mm).
  • rain_3h: rain in last 3 hours (mm).
  • snow_3h: show last 3 hours (mm).
  • clouds_all: cloud cover in percentage.
Import data 
dir_data <- "../grenfin-summer-school/data"
filepath <- file.path(dir_data, "data.csv")
data <- readr::read_csv(filepath, show_col_types = FALSE, progress = FALSE)
head(data) %>%
  knitr::kable(booktabs = TRUE ,escape = FALSE, align = 'c')%>%
  kableExtra::row_spec(0, color = "white", background = "green")
date date_day Year Month Day Hour Season fossil nuclear energy_other solar biomass river energy_other_renewable energy_waste wind pred_solar pred_demand pred_price demand price prod prod_renewable temp temp_min temp_max pressure humidity wind_speed wind_deg rain_1h rain_3h snow_3h clouds_all
2014-12-31 23:00:00 2014-12-31 2014 12 31 23 Winter 10156 7096 43 49 447 3813 73 196 6378 17 26118 50.10 25385 65.41 27939 10687 -0.6585375 -5.825 8.475 1016.4 82.4 2.0 135.2 0 0 0 0
2015-01-01 00:00:00 2015-01-01 2015 1 1 0 Winter 10437 7096 43 50 449 3587 71 195 5890 16 24934 48.10 24382 64.92 27509 9976 -0.6373000 -5.825 8.475 1016.2 82.4 2.0 135.8 0 0 0 0
2015-01-01 01:00:00 2015-01-01 2015 1 1 1 Winter 9918 7099 43 50 448 3508 73 196 5461 8 23515 47.33 22734 64.48 26484 9467 -1.0508625 -6.964 8.136 1016.8 82.0 2.4 119.0 0 0 0 0
2015-01-01 02:00:00 2015-01-01 2015 1 1 2 Winter 8859 7098 43 50 438 3231 75 191 5238 2 22642 42.27 21286 59.32 24914 8957 -1.0605312 -6.964 8.136 1016.6 82.0 2.4 119.2 0 0 0 0
2015-01-01 03:00:00 2015-01-01 2015 1 1 3 Winter 8313 7097 43 42 428 3499 74 189 4935 9 21785 38.41 20264 56.04 24314 8904 -1.0041000 -6.964 8.136 1016.6 82.0 2.4 118.4 0 0 0 0
2015-01-01 04:00:00 2015-01-01 2015 1 1 4 Winter 7962 7098 43 34 410 3804 74 188 4618 4 21441 35.72 19905 53.63 23926 8866 -1.1260000 -7.708 7.317 1017.4 82.6 2.4 174.8 0 0 0 0
R packages 
library(tidyverse)
library(backports)
library(solarr)
library(latex2exp)

3 Project

3.1 Problem A. Explorative analysis

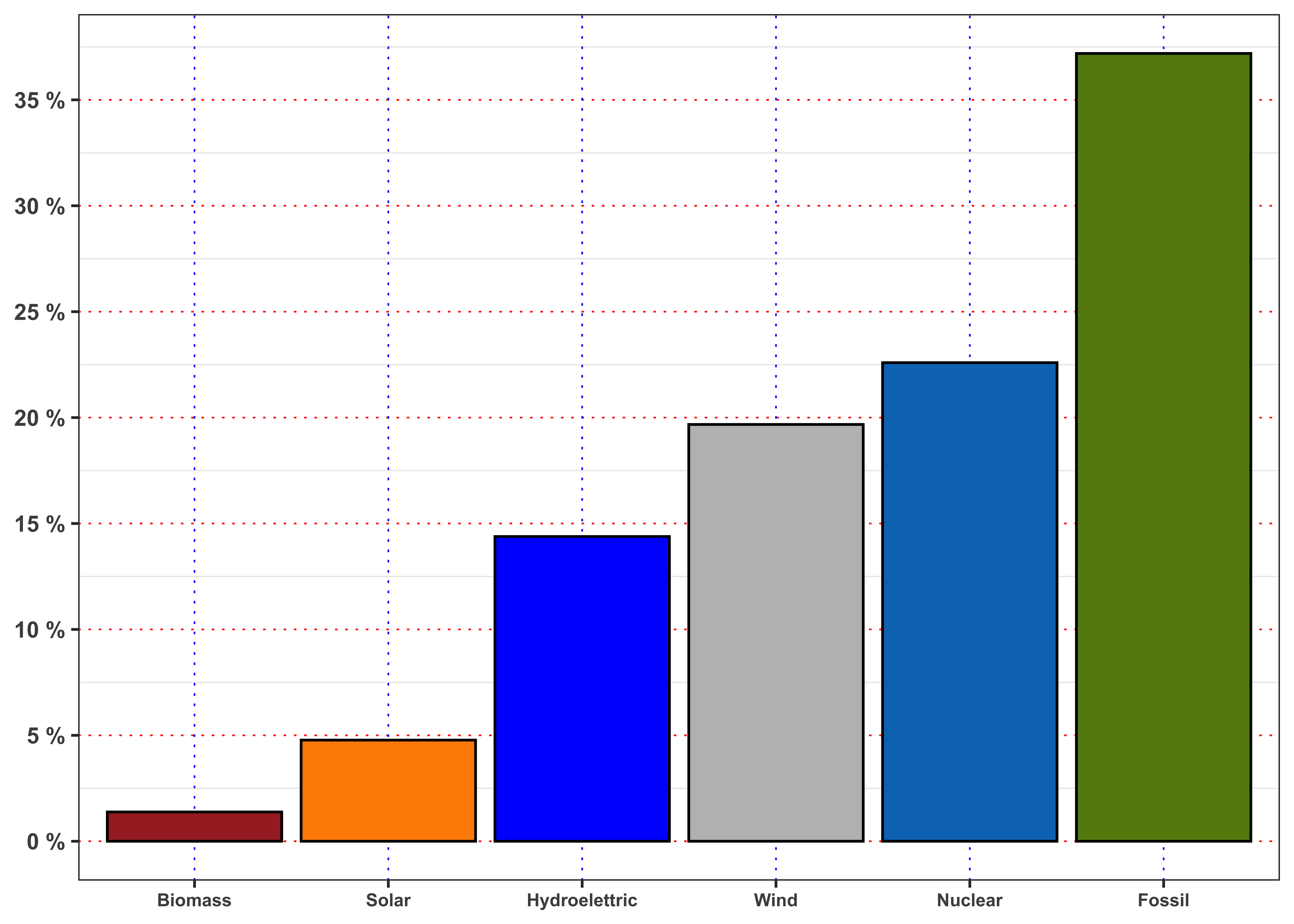
Consider the data of the energy market in Spain and let’s examine the composition of the energy mix. At your disposal you have 5 sources that generate energy, i.e. 4 renewable (columns biomass, solar, river, wind) and 2 non-renewable (columns nuclear, fossil). The column demand denotes the amount of demanded electricity in MW, instead the column price denotes the actual price in \(MW/h\). For simplicity, let’s denote with \(E^{\boldsymbol{\ast}}_{t}\) the energy of the \(\boldsymbol{\ast}\)-th source, i.e.  \[ E^{\boldsymbol{\ast}}_{t} = \begin{cases} E^{b}_{t} \quad \boldsymbol{\ast} \to b = \text{biomass} \\ E^{s}_{t} \quad \boldsymbol{\ast} \to s = \text{solar} \\ E^{h}_{t} \quad \boldsymbol{\ast} \to h = \text{hydroelettric} \\ E^{w}_{t} \quad \boldsymbol{\ast} \to w = \text{wind} \\ E^{n}_{t} \quad \boldsymbol{\ast} \to n = \text{nuclear} \\ E^{f}_{t} \quad \boldsymbol{\ast} \to f = \text{fossil} \\ \end{cases} \] and the total energy demanded at time \(t\) as \(D_t\).

3.1.1 Task A.1

Compute the average between the energy produced from each source and the total demand, i.e.
\[ R^{{\boldsymbol{\ast}}} = \frac{1}{n} \sum_{t = 1}^{n} \frac{E^{\boldsymbol{\ast}}_{t}}{D_{t}} \tag{1}\]

and normalize them, i.e. \(R^{\boldsymbol{\ast}}/\sum R^{\boldsymbol{\ast}}\). Rank the 5 sources of energy by the percentage of demand satisfied in decreasing order and plot the values obtained with histograms.

3.1.2 Task A.2

Aggregate the sources of energy in two groups:

  1. Renewable: is given by the sum of solar, river, wind and biomass.
  2. Non-renewable: is given by the sum of nuclear and fossil.

Then, compute the percentage of energy demand satisfied by each group. What is the percentage of energy satisfied by renewable sources? And by the fossil ones?

Repeat the computations, but filtering the data firstly only for year 2015 and then only for 2018. Are the percentage obtained different? Describe the result and explain if the transition to renewable energy is supported by data (to be supported the percentage of renewable energy should increase while percentage of fossil fuels should decrease.)

3.1.3 Task A.3

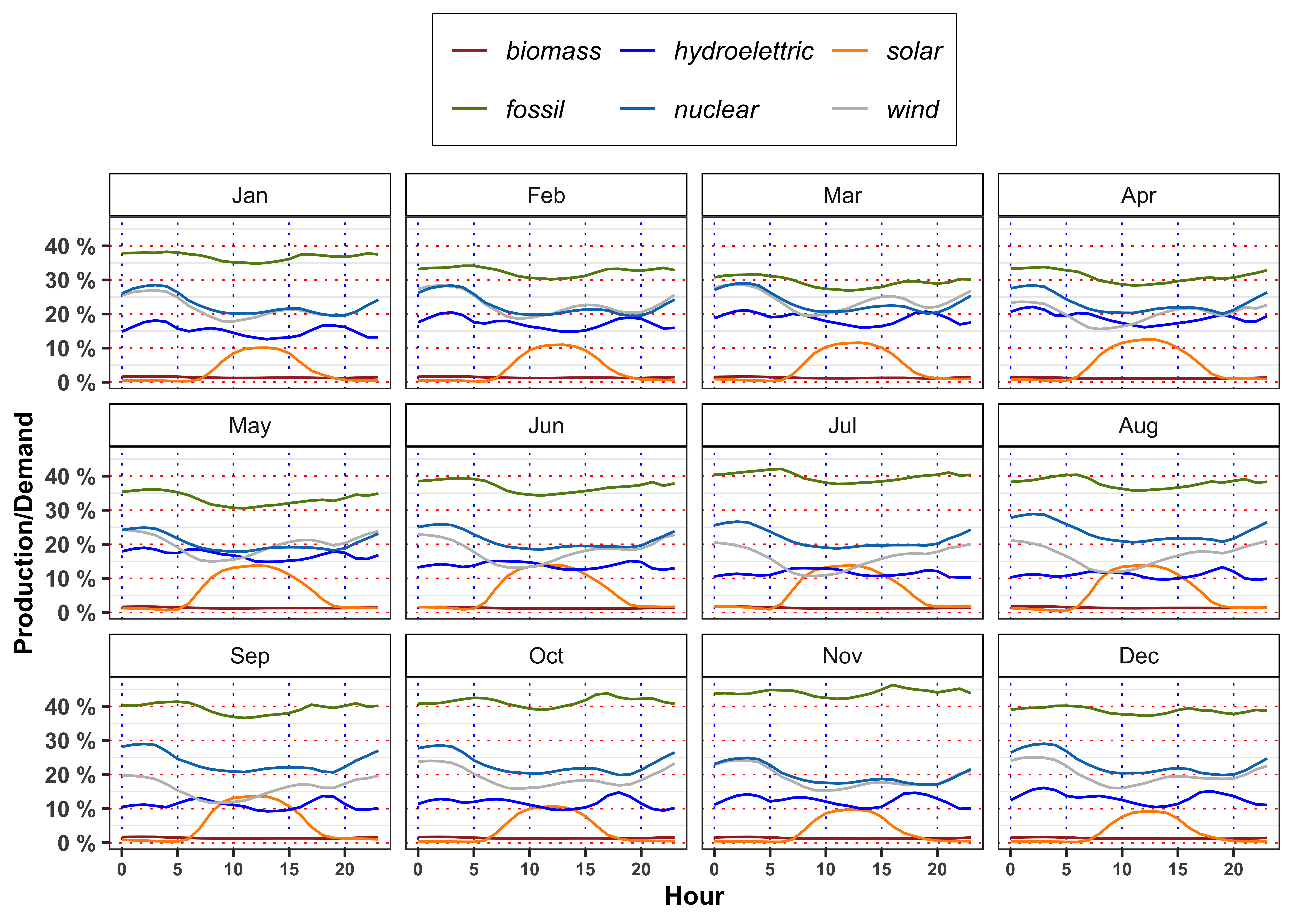
For each month, compute the mean percentage of demand of energy satisfied by the fossil sources. In order to compute \(R^{{\boldsymbol{\ast}}}_m\) for the \(m\)-month, let’s denote with \(n_m\) the number of day in that month, then: \[ R^{{\boldsymbol{\ast}}}_m = \frac{1}{n_m} \sum_{t = 1}^{n_m} \frac{E^{\boldsymbol{\ast}}_{t}}{D_{t}} = \frac{1}{n_m} \sum_{t = 1}^{n_m} R^{{\boldsymbol{\ast}}}_t \tag{2}\]

Compute also the maximum, minimum, median and standard deviation of \(R^{{\boldsymbol{\ast}}}_t\) for each month. Repeat the computation for the others 4 sources of energy, i.e. nuclear, solar, river and wind. Which are the source with the lowest and the highest standard deviation in December? And in June? Comment the results obtained (max 200 words).

3.1.4 Task A.4

In mean, the demand satisfied by solar energy with respect to total demand is greater or lower with respect to the one satisfied by hydroelectric on 12:00 in March? In July, August and September at the same hour the situation changes? Answer, providing a possible explanation of the results obtained (max 200 words).

3.1.5 Task A.5

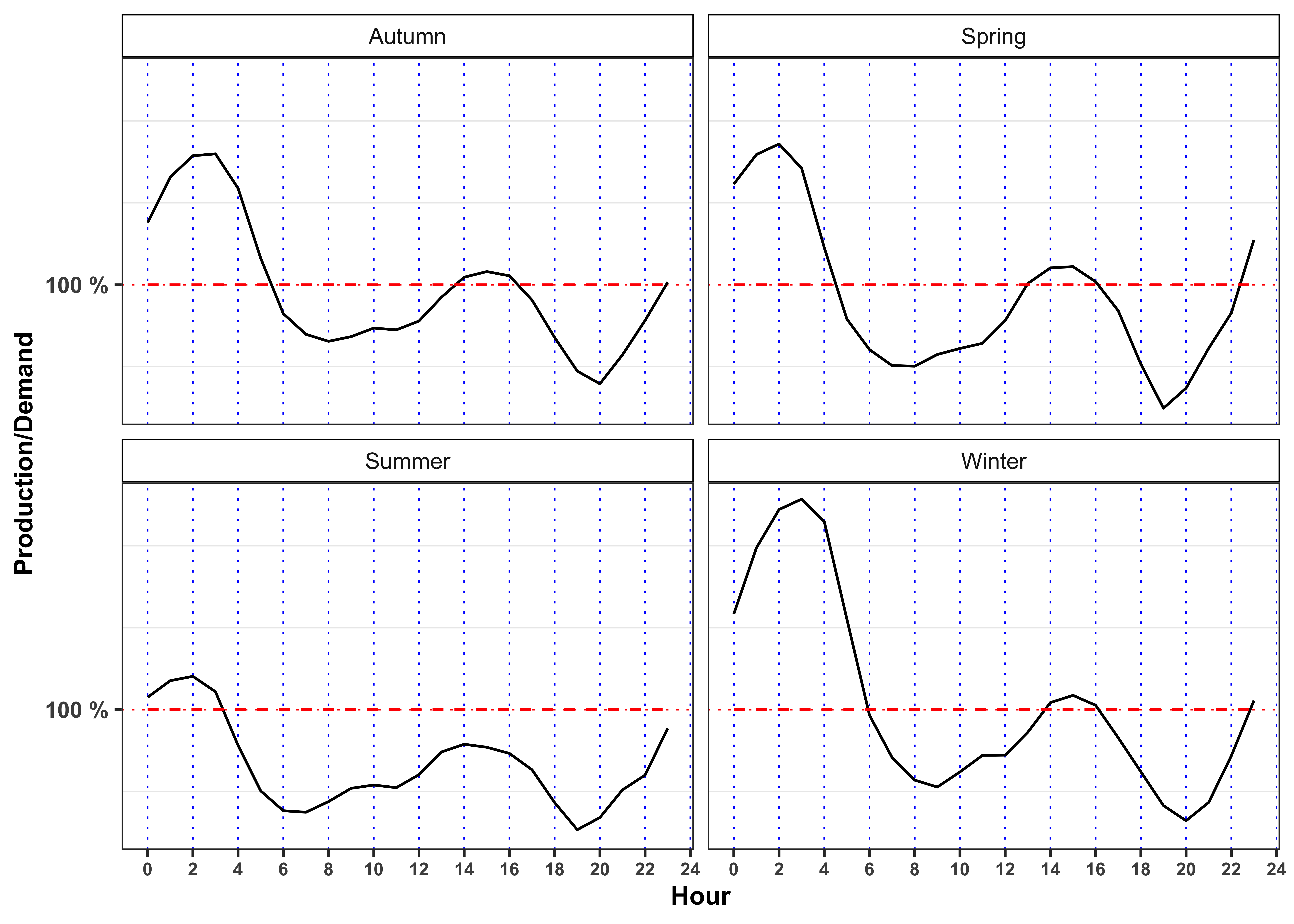
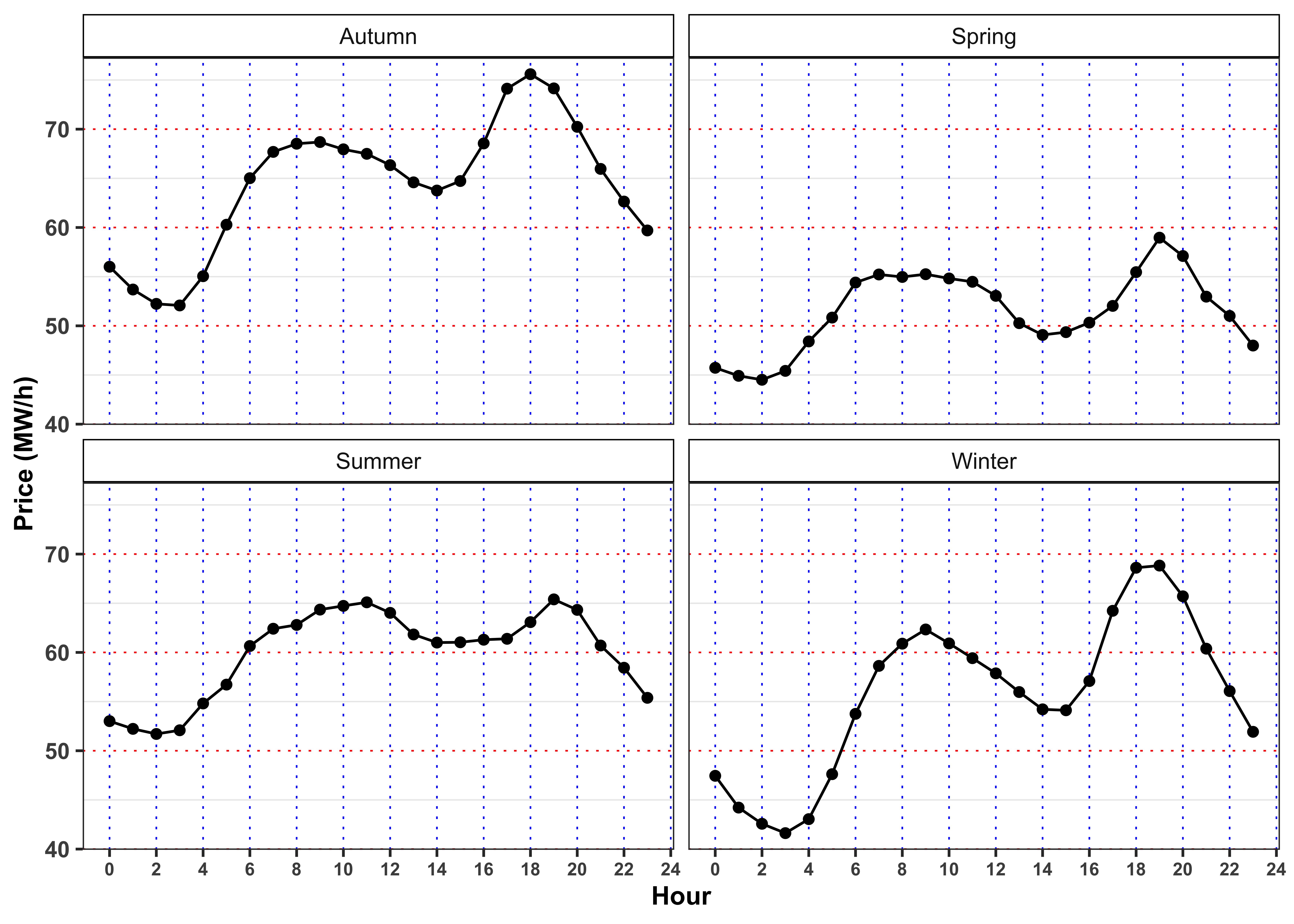
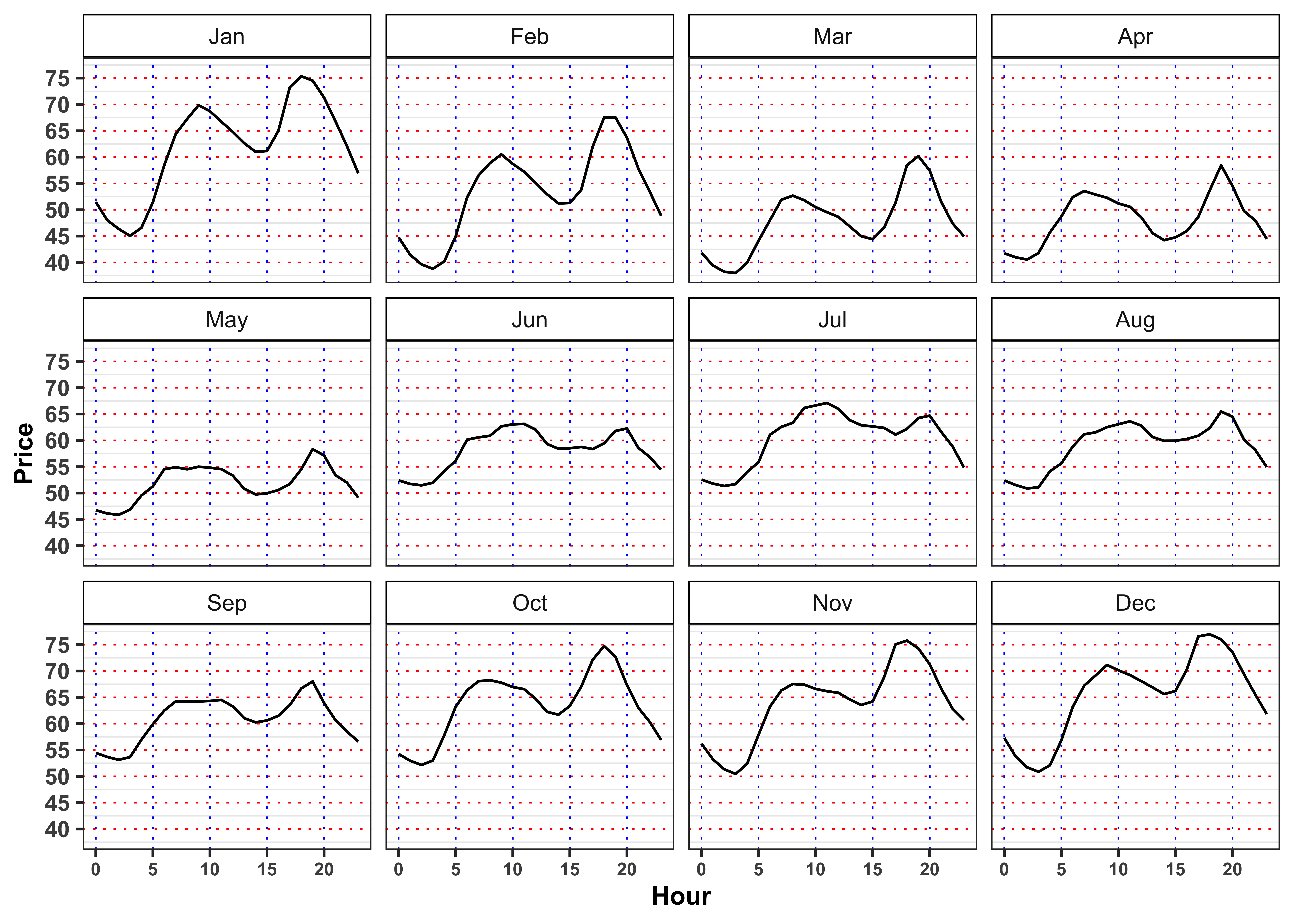
Grouping the dataset firstly by season and hour (\(4 \times 24\) groups) and then by month and hour (\(12 \times 24\) groups) compute:

  1. Average electricity price
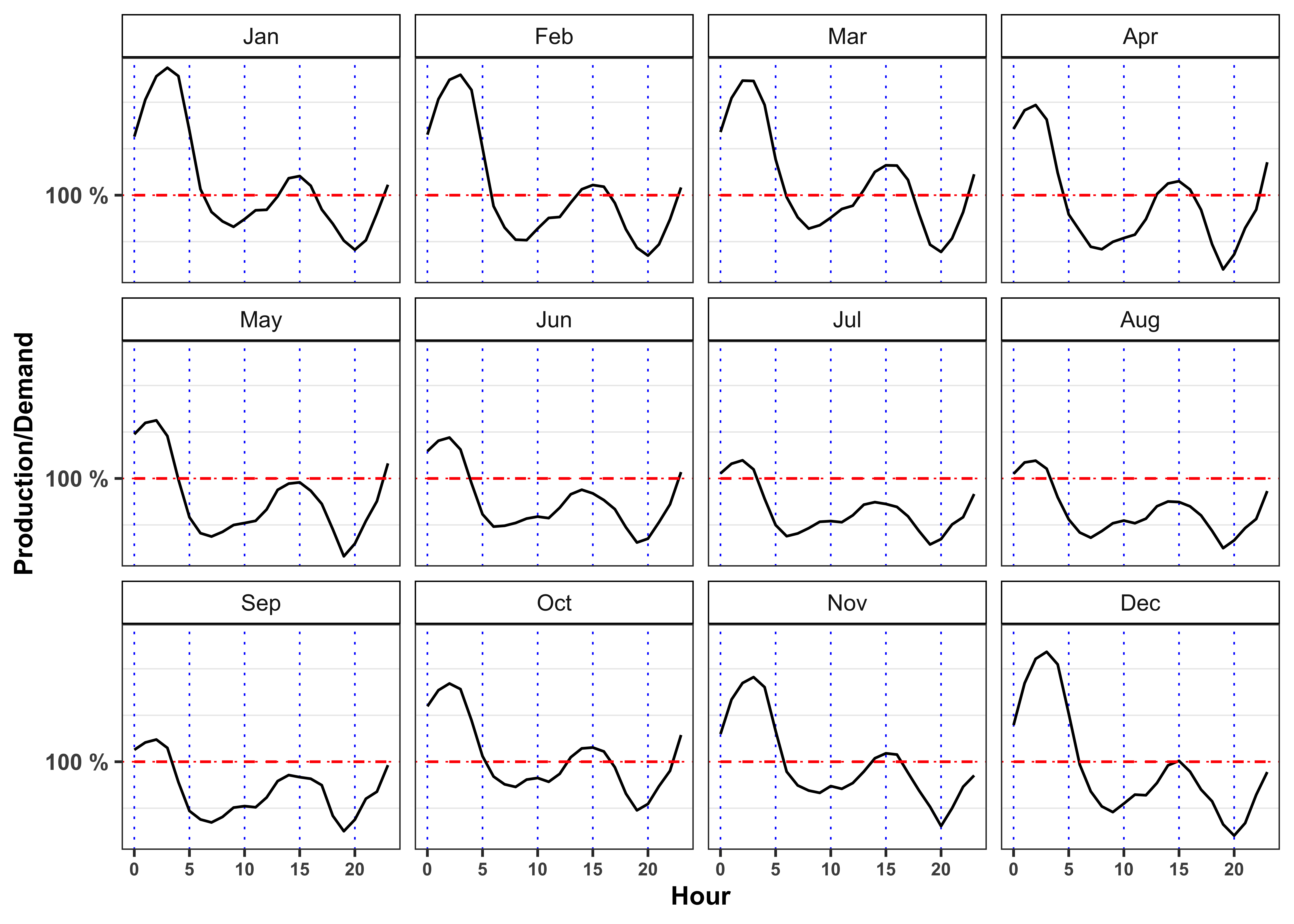
  2. Average ratio between total production and total demand, i.e. prod/demand.

For both groups, answer to the following questions.

What is the meaning of a ratio between total production and total demand greater than 1? And greater than 1? Following the demand and supply law, what is the expected behavior of the price in such situations? Comment the results (max 200 words).

When the price reaches it’s minimum value? In such situation, does the ratio reach its maximum value? What happen when the prices reaches it’s maximum? Comment the results (max 200 words).

3.2 Problem B: Model hourly electricity price

3.2.1 Task B.1

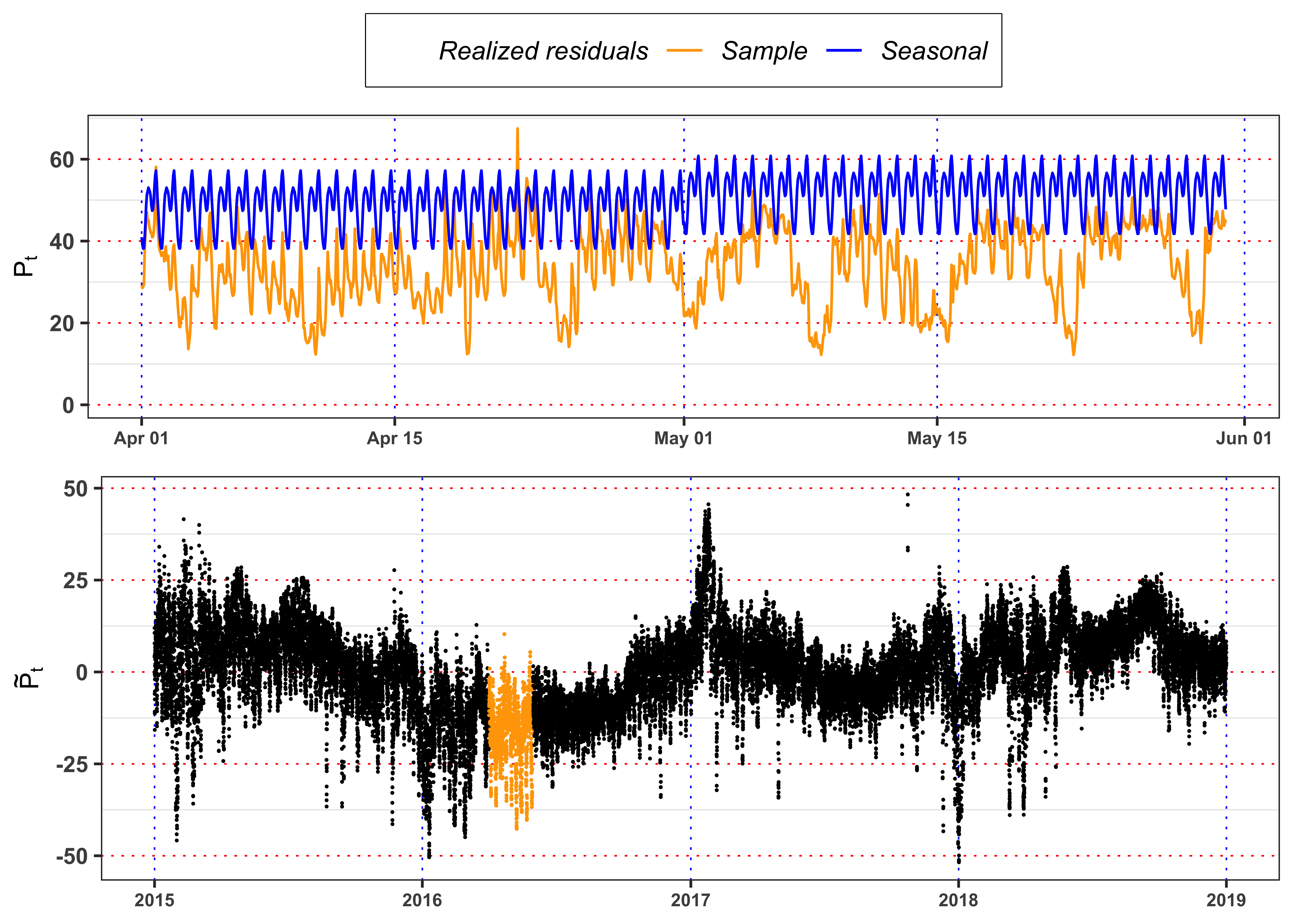
Let’s define and estimate a model for the hourly electricity price. First of all, we have to define a seasonal function to remove deterministic patterns during the year and the day. Hence, we take into account a function of the form: \[ \begin{aligned} \bar{P}_t = p_0 + H(t) + M(t) \end{aligned} \] where \(H(t)\) stands for: \[ H(t) = \begin{cases} H_1 \quad \ \text{Hour} = 1 \\ H_2 \quad \ \text{Hour} = 2 \\ \vdots \\ H_{23} \quad \text{Hour} = 23 \\ \end{cases} \] and \(M(t)\) for: \[ M(t) = \begin{cases} M_2 \quad \ \text{Month} = \text{February} \\ \vdots \\ M_{12} \quad \text{Month} = \text{December} \\ \end{cases} \] It follows that, by construction, \(p_0\) captures the \(\text{Hour} = 0\) and \(\text{Month} = \text{January}\). Estimate the parameters of the models using OLS. Then, compute the seasonal price \(\bar{P}_t\) and the deseasonalized time series, i.e.  \[ \tilde{P}_t = P_t - \bar{P}_t \] Plot \(\bar{P}_t\) and \(\tilde{P}_t\).

3.2.2 Task B.2

Estimate an autoregressive model (AR(1)) on the deseasonalized time series, i.e. \[ \begin{aligned} \tilde{P}_t = \phi \tilde{P}_{t-1} + \varepsilon_t \end{aligned} \] Is the estimated model stationary? Comment and justify your answer.

Hint: in order to answer consider the stationarity condition on the parameters.

Then, compute the fitted residuals \(\varepsilon_t\) and their standard deviation as: \[ \bar{\sigma} = \mathbb{S}d\{\varepsilon_t\} = \sqrt{\frac{1}{n-1}\sum_{t = 1}^n \varepsilon_t^2} \text{,} \] and the standardized residuals as \[ \bar{\varepsilon_t} = \frac{\varepsilon_t}{\bar{\sigma}} \text{.} \] Are \(\bar{\varepsilon_t}\) identically distributed? Answer with a formal statistics test with confidence level \(\alpha = 0.05\). (see for example see the two sample Kolmogorov-Smirnov test).

3.2.3 Task B.3

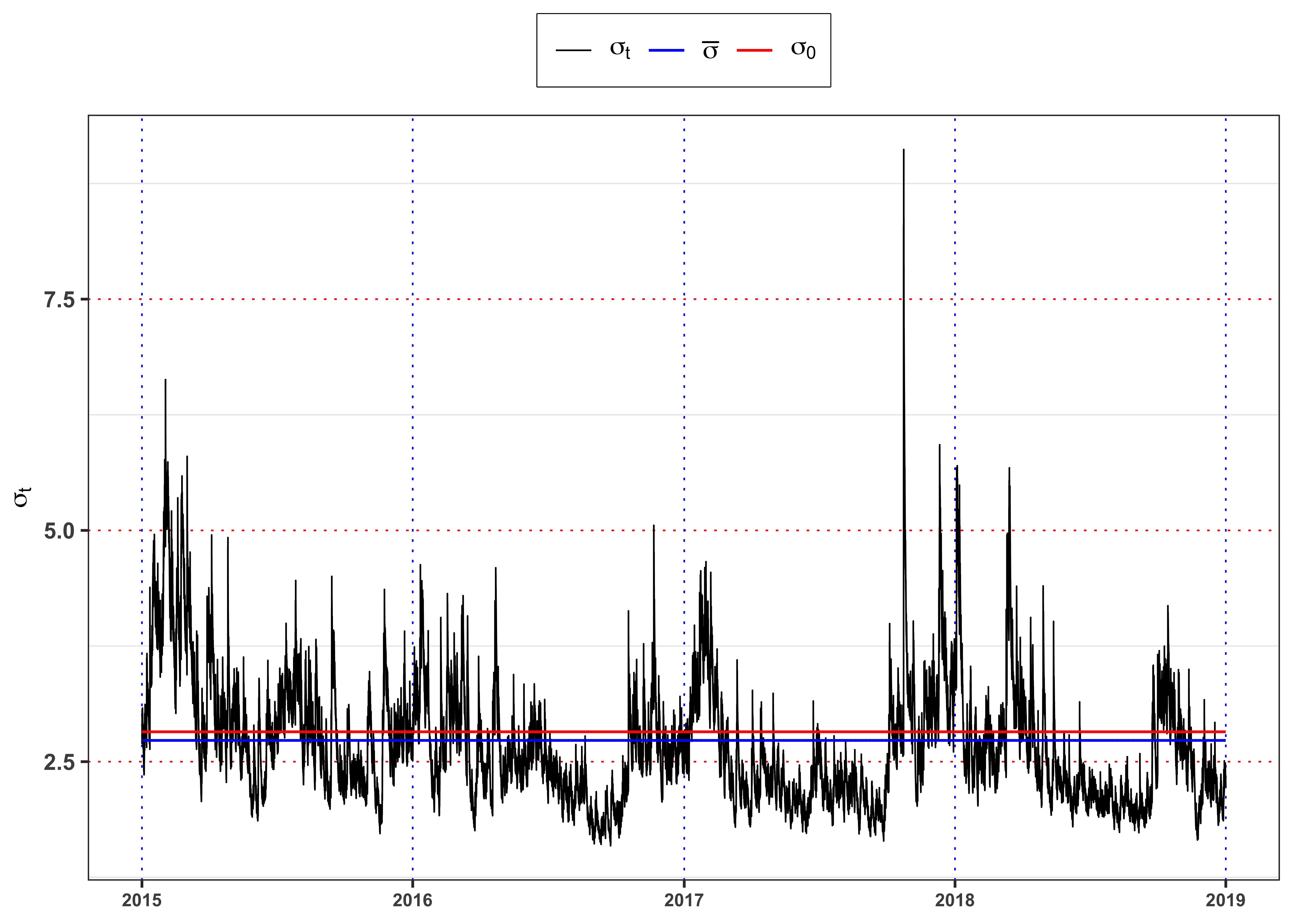
A model for the conditional variance is the GARCH(p,q) model. Let’s consider a GARCH(1,2) model under the normality assumption., i.e.  \[ \begin{aligned} & {}\varepsilon_t = \sigma_{t} u_t \\ & \sigma_{t}^2 = \omega + \alpha_1 \varepsilon_{t-1}^2 + \beta_1 \sigma_{t-1}^2 + \beta_2 \sigma_{t-2}^2 \\ & u_{t} \sim \; \mathcal{N}(0, 1) \end{aligned} \]

Is the estimated model stationary? Hint: in order to answer consider the stationarity condition on the parameters.

Compute the long-term variance under the GARCH(1,1) model, i.e. \(\mathbb{E}\{\sigma_t^2\}\), and compare it with the variance estimated in Task B.2 (i.e. \(\bar{\sigma}^2\)). Are the two variances similar? Comment the results.

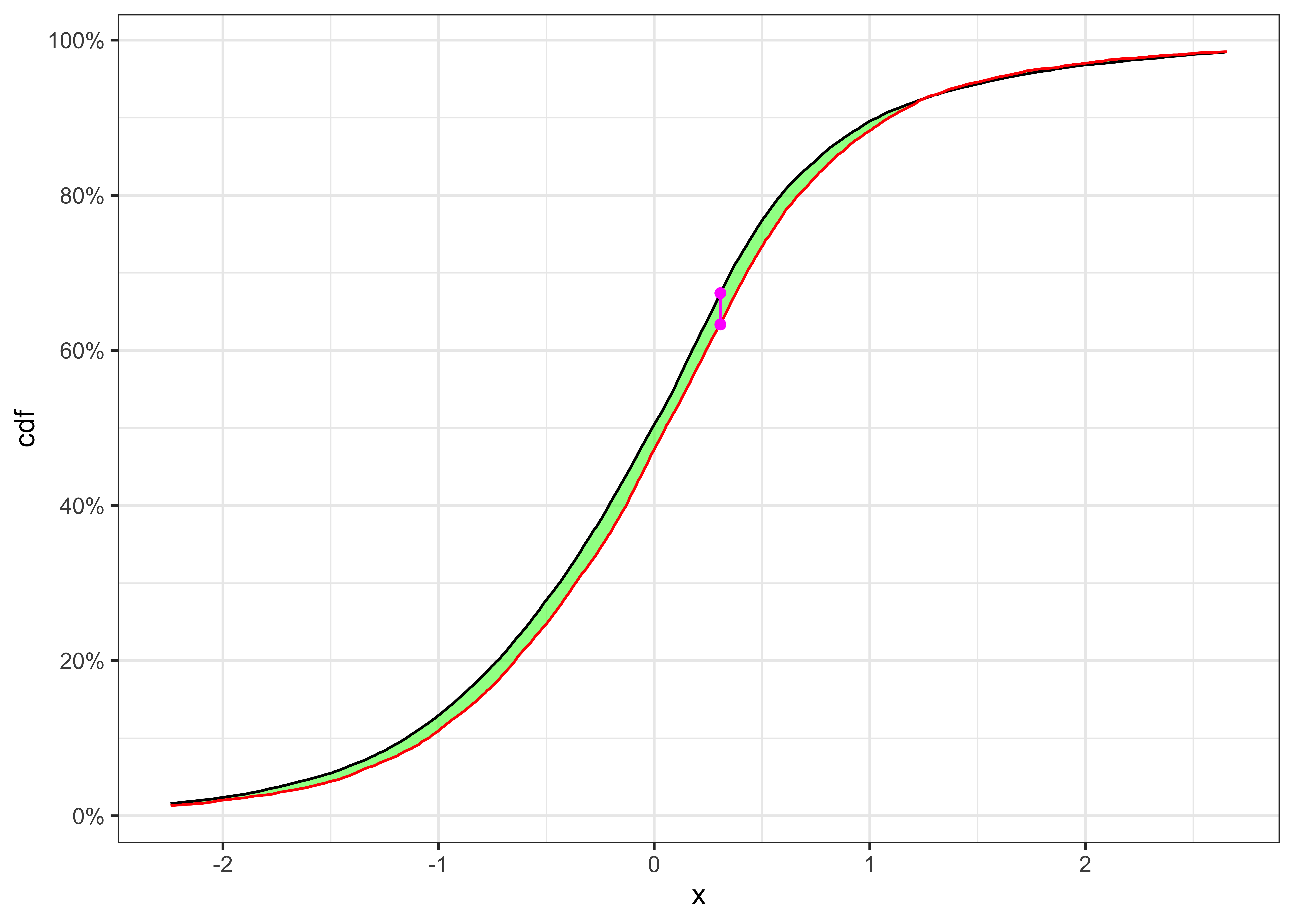
Define the standardized GARCH residuals as: \[ u_t = \frac{\varepsilon_t}{\sigma_t} \] Are now the standardized residuals identically distributed? Answer using the same test used in Task B.2. Is the normality assumption satisfied on the fitted residuals? Answer with a formal test and a \(\alpha = 0.01\).

Hint: see for example see the Kolmogorov-Smirnov test.

3.2.4 Task B.4

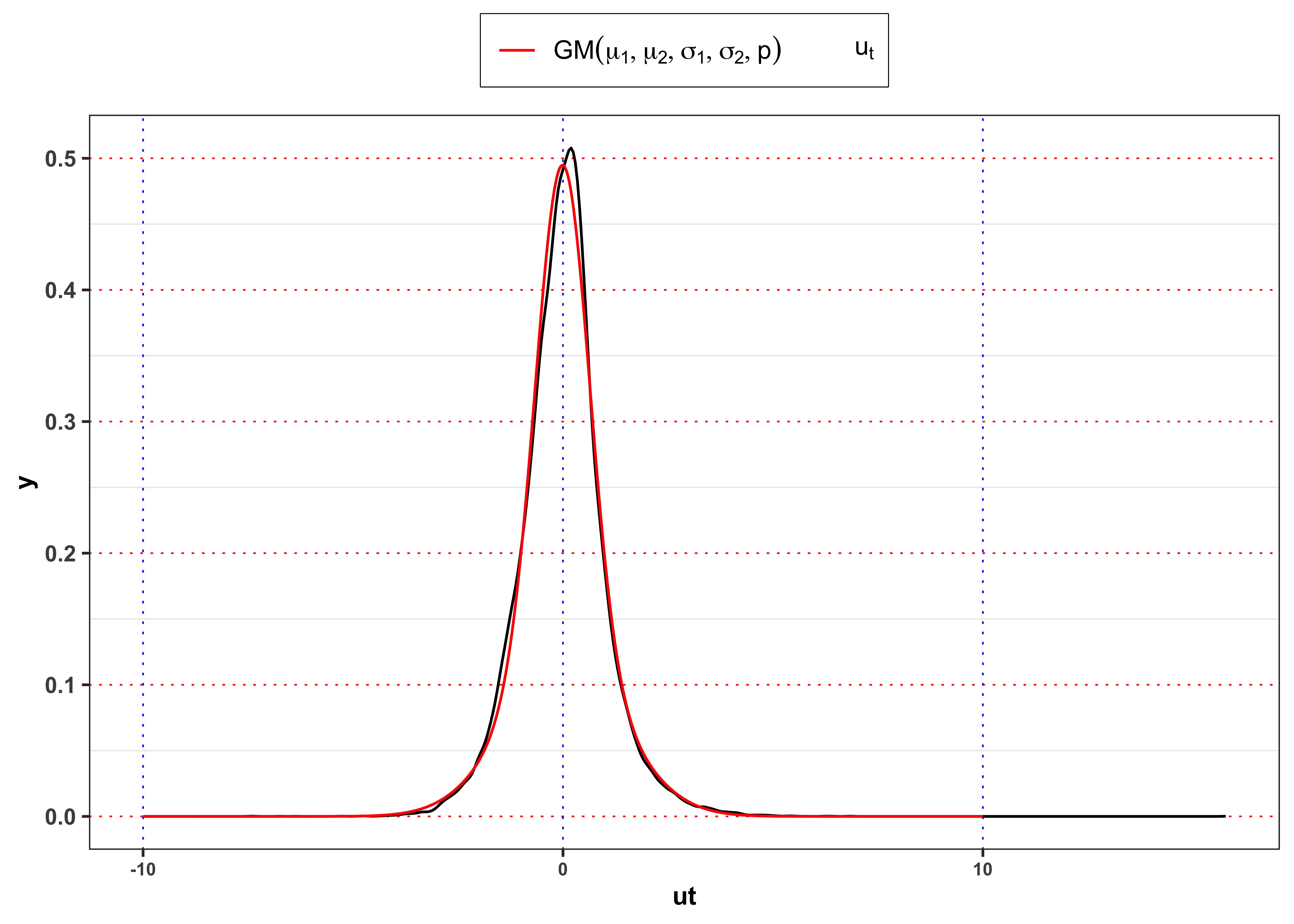
Let’s consider a Gaussian mixture model for the GARCH residuals, i.e.  \[ u_t \sim B \cdot (\mu_{1} + \sigma_{1} Z_1) + (1-B) \cdot (\mu_{2} + \sigma_{2} Z_2) \]

where \(B \sim \text{Bernoulli}(p)\), while \(Z_1\) and \(Z_2\) are standard normal. All are assumed to be independent. Estimate the parameters \(\mu_{1}\), \(\mu_{2}\), \(\sigma_{1}\), \(\sigma_{2}\) and \(p\) with maximum likelihood (see here for an example). Consider the estimated parameters and give a possible interpretation of the two states, i.e. B = 1, B = 0.

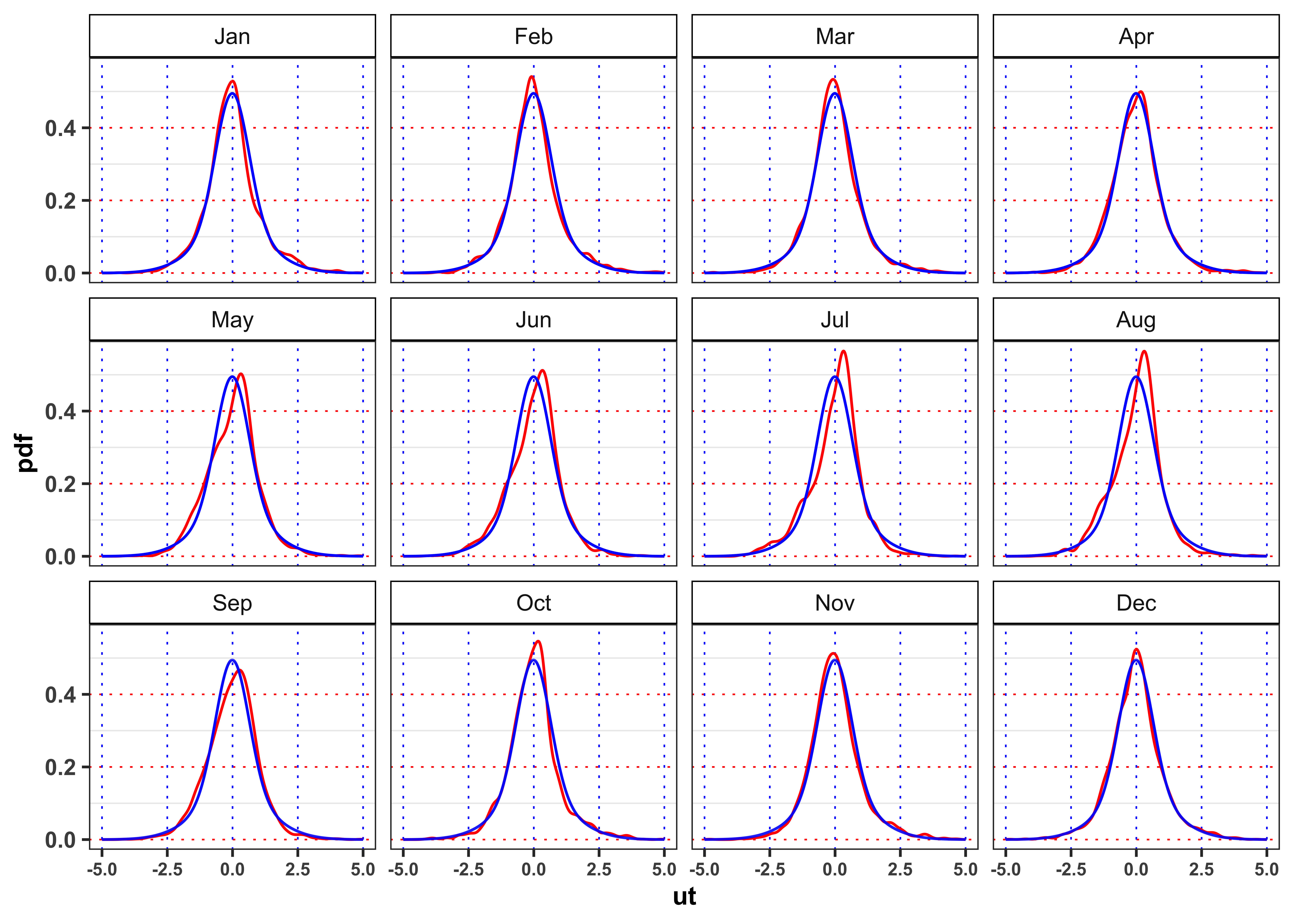
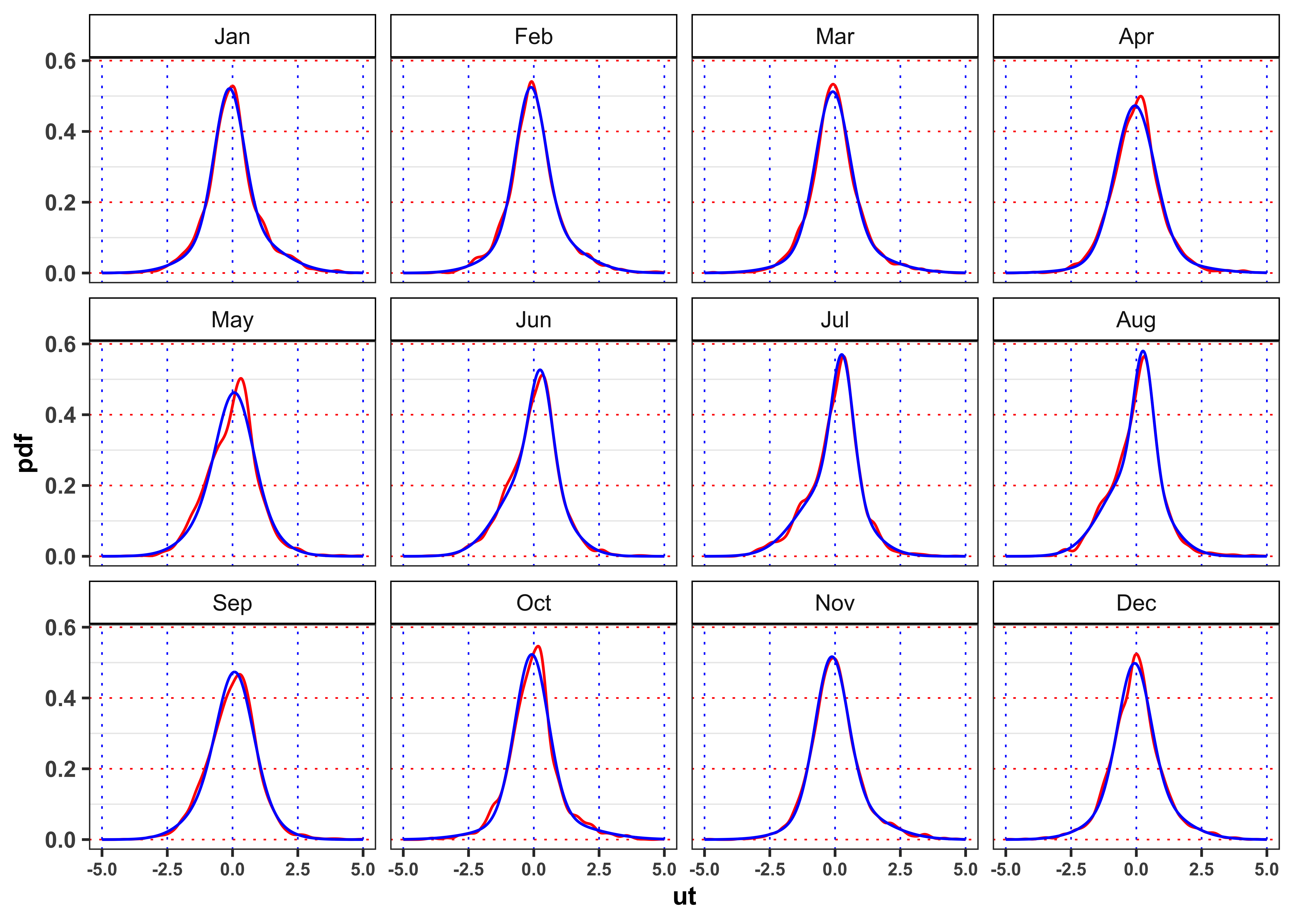
3.2.5 Task B.5

Let’s consider a monthly Gaussian mixture model for the GARCH residuals \(u_{t, m}\), where the index \(m = 1, \dots, 12\) denotes the \(m\)-month, i.e. \[ u_{t,m} \sim B_m \cdot Z_{m,1} + (1-B_m) \cdot Z_{m,2} \] where all the random variables, i.e.  \[ \begin{aligned} {} & B_m \sim \text{Bernoulli}(p_m) \\ & Z_{m,1} = \mathcal{N}(\mu_{m,1},\sigma_{m,1}^2) \\ & Z_{m,2} = \mathcal{N}(\mu_{m,2},\sigma_{m,2}^2) \end{aligned} \] are assumed to be independent. Estimate the parameters for all the months with maximum likelihood.

3.2.6 Task B.6

Let’s simulate hourly prices with the model and compare it with the empirical ones. You are free to choose between the basic Gaussian mixture and the monthly version. Then, consider the following two situations:

  1. Projection A: You are 2017-06-28 (known) and you want to simulate 100 trajectories for the price from 2017-06-29 up to 2017-06-30 (1 day, 24 hours).

  2. Projection B: You are in 2017-12-01 (known) and you want to simulate 100 trajectories for the price from 2017-12-02 up to 2017-12-31 (29 days, 696 hours).

Be careful in simulations to always set a seed for reproducibility.

  • The distribution of the residuals in the Projection A are close to the empirical distribution of the residuals in that month? The situation in Projection B changes? Is the model able to forecast the short term movements of the electricity price? Comment the results.

Hint 1: For a graphical comparison between densities you can plot the empirical histograms of \(u_t\) for the month \(m = 12\) (December) and the histograms of the simulated \(u_t\) for the same month.

Hint 2: Think about the fact that the aim of our model is to try to reproduce the distribution of the electricity prices and not to forecast it’s short term movements (potential omitted values could improve the model performances).

Back to top

Citation

BibTeX citation:
@online{sartini2025,
  author = {Sartini, Beniamino},
  date = {2025-06-21},
  url = {https://greenfin.it/projects/project2024.html},
  langid = {en}
}
For attribution, please cite this work as:
Sartini, Beniamino. 2025. June 21, 2025. https://greenfin.it/projects/project2024.html.